
| A. | [$\frac{1}{{e}^{2}}$,$\frac{1}{2e}$) | B. | [$\frac{1}{2e}$,$\frac{1}{e}$] | C. | (0,$\frac{1}{{e}^{2}}$) | D. | ($\frac{1}{e}$,+∞) |
分析 化简可得k=$\frac{lnx}{{x}^{2}}$,从而令t(x)=$\frac{lnx}{{x}^{2}}$,求导t′(x)=$\frac{1-2lnx}{{x}^{3}}$=0,从而解得t(x)在[$\frac{1}{e}$,$\sqrt{e}$]上单调递增,在[$\sqrt{e}$,e]上单调递减;从而解得.
解答 解:由f(x)=g(x)得,k=$\frac{lnx}{{x}^{2}}$,令t(x)=$\frac{lnx}{{x}^{2}}$,
由t′(x)=$\frac{1-2lnx}{{x}^{3}}$=0得x=$\sqrt{e}$,
故t(x)在[$\frac{1}{e}$,$\sqrt{e}$]上单调递增,
在[$\sqrt{e}$,e]上单调递减,
又t($\sqrt{e}$)=$\frac{1}{2e}$,t($\frac{1}{e}$)=-e2,t(e)=$\frac{1}{{e}^{2}}$,
故?xi∈[$\frac{1}{e}$,e],(i=1,2)使得f(xi)=g(xi),(i=1,2),
则实数k的取值范围是[$\frac{1}{{e}^{2}}$,$\frac{1}{2e}$),
故选:A.
点评 本题考查了方程的根与函数的零点的关系应用及导数的综合应用.


科目:高中数学 来源: 题型:解答题
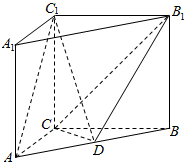 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=CC1=2,AC⊥BC,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30尺 | B. | 90尺 | C. | 150尺 | D. | 180尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
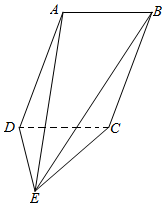 如图,平行四边形ABCD⊥平面CDE,AD=DC=DE=4,∠ADC=60°,AD⊥DE
如图,平行四边形ABCD⊥平面CDE,AD=DC=DE=4,∠ADC=60°,AD⊥DE查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com