练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知在△ABC中，AB=4，AC=6，BC=$\sqrt{7}$，其外接圆的圆心为O，则$\overrightarrow{AO}$$•\overrightarrow{BC}$10．

    分析 根据向量数量积的几何意义即可得到答案．

    解答 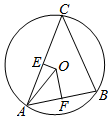解：$\overrightarrow{AO}$$•\overrightarrow{BC}$=$\overrightarrow{AO}$（$\overrightarrow{AC}$$-\overrightarrow{AB}$）=$\overrightarrow{AO}•\overrightarrow{AC}$-$\overrightarrow{AO}$•$\overrightarrow{AB}$，
    如图，根据向量数量积的几何意义得）$\overrightarrow{AO}•\overrightarrow{AC}$-$\overrightarrow{AO}$•$\overrightarrow{AB}$=6|$\overrightarrow{AE}$|-4|$\overrightarrow{AF}$|=6×3-4×2=10，
    故答案为：10．

    点评 本小题主要考查向量在几何中的应用等基础知识，解答关键是利用向量数量积的几何意义．属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    8．命题$p：?x∈（0，\frac{π}{2}），f（x）＜0$，则?p：$?x∈（0，\frac{π}{2}），f（x）≥0$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知直线l：y=kx与椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$交于A、B两点，其中右焦点F的坐标为（c，0），且AF与BF垂直，则椭圆C的离心率的取值范围为（　　）
    A．$[{\frac{{\sqrt{2}}}{2}，1}）$B．$（{0，\frac{{\sqrt{2}}}{2}}]$C．$（{\frac{{\sqrt{2}}}{2}，1}）$D．$（{0，\frac{{\sqrt{2}}}{2}}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知函数f（x）=kx，g（x）=$\frac{lnx}{x}$，若?xi∈[$\frac{1}{e}$，e]，（i=1，2）使得f（xi）=g（xi），（i=1，2），则实数k的取值范围是（　　）
    A．[$\frac{1}{{e}^{2}}$，$\frac{1}{2e}$）B．[$\frac{1}{2e}$，$\frac{1}{e}$]C．（0，$\frac{1}{{e}^{2}}$）D．（$\frac{1}{e}$，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知等比数列{an}满足a1+a3+a7=22，a5+a7+a11=88，则a7+a9+a13=（　　）
    A．121B．154C．176D．352

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$的右焦点为F，P是椭圆上一点，点$A（{0，2\sqrt{3}}）$，当△APF的周长最大时，△APF的面积等于（　　）
    A．$\frac{{11\sqrt{3}}}{4}$B．$\frac{{21\sqrt{3}}}{4}$C．$\frac{11}{4}$D．$\frac{21}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．设点O在△ABC的内部，点D，E分别为边AC，BC的中点，且$|{\overrightarrow{OD}+2\overrightarrow{DE}}|=1$，则$|{\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}}|$=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知对数函数f（x）=logax，若f-1（2）=$\frac{1}{4}$，则a=$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．若函数 f（x）=ae-x-ex为奇函数，则f（x-1）＜e-$\frac{1}{e}$的解集为（　　）
    A．（-∞，0）B．（-∞，2）C．（2，+∞）D．（0，+∞）

    查看答案和解析>>

    同步练习册答案