
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 要求一个函数零点,只要使得这个函数等于0,把其中一个移项,得到两个基本初等函数,在规定的范围中画出函数的图象,看出交点的个数.
解答 解:∵f(x)=tanx-sinx,故有f(0)=0,即0是f(x)在区间(-$\frac{π}{2}$,$\frac{π}{2}$)上的一个零点.
根据正弦曲线和正切曲线,可得两个函数都是奇函数,
只要看出两个曲线在区间(0,$\frac{π}{2}$)上的交点个数就可以了.
由于在区间(0,$\frac{π}{2}$)上,由图象可得sinx<tanx,
故f(x)=tanx-sinx在区间(0,$\frac{π}{2}$)上无零点,故f(x)在(-$\frac{π}{2}$,0)无也零点.
综上可得,函数f(x)=tanx-sinx在区间(-$\frac{π}{2}$,$\frac{π}{2}$)上有1个零点.
同理,函数在(-$\frac{3}{2}$π,-$\frac{π}{2}$),($\frac{π}{2}$,$\frac{3}{2}$π)各有一个零点.
故选:C.
点评 本题考查函数零点的定义和判定方法,函数的奇偶性的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
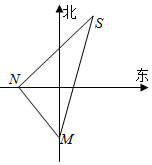 如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( )
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( )| A. | 20($\sqrt{2}$+$\sqrt{6}$)n mile/h | B. | 20($\sqrt{6}$-$\sqrt{2}$)n mile/h | C. | 20($\sqrt{3}$+$\sqrt{6}$)n mile/h | D. | 20($\sqrt{6}$-$\sqrt{3}$)n mile/h |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
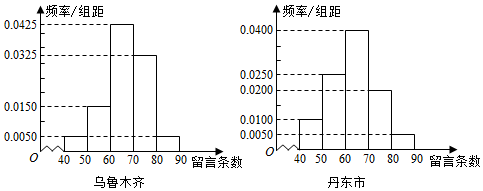
| 强烈关注 | 非强烈关注 | 合计 | |
| 丹东市 | 15 | 45 | 60 |
| 乌鲁木齐市 | 15 | 25 | 40 |
| 合计 | 30 | 70 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com