练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．若f（x）=${e}^{-\frac{1}{x}}$，则$\underset{lim}{t→∞}\frac{f（1-2t）-f（1）}{t}$=-2e-1．

    分析 利用导数的定义对所求变形，得到实际所求，然后求已知函数的导数

    解答 解：$\underset{lim}{t→∞}\frac{f（1-2t）-f（1）}{t}$=-2$\underset{lim}{\frac{1}{t}→0}\frac{f（1-\frac{2}{t}）-f（1）}{\frac{-2}{t}}$=-2f'（1），
    又f（x）=${e}^{-\frac{1}{x}}$，所以f'（x）=（${e}^{-\frac{1}{x}}$）'=$\frac{1}{{x}^{2}}{e}^{-\frac{1}{x}}$，
    所以f'（1）=e-1；
    故答案为：-2e-1．

    点评 本题考查了导数的定义的运用以及复合函数求导；属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    11．已知函数f（x）=$\left\{\begin{array}{l}{（1-2a）^{x}，x≤1}\\{lo{g}_{a}x+\frac{1}{3}，x＞1}\end{array}\right.$，对任意实数x1，x2，当x1≠x2时，都有$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＜0，则a的取值范围是（0，$\frac{1}{3}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

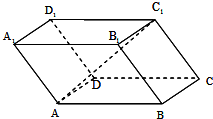    8．已知平行六面体ABCD-A1B1C1D1中，底面ABCD是边长为2的正方形，侧棱AA1的长为2，∠A1AB=∠A1AD=120°．
    求：（1）直线A1C和BB1的夹角的余弦值；
    （2）设|A1C|=a，|A1B|=b，|A1D|=c请设计一个算法，当输入实数a，b，c，要求输出这三个数中最大的数，请写出算法并画出程序框图．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知函数f（x）=$\sqrt{lo{g}_{2}（x-1）}$的定义域为A，函数g（x）=（$\frac{1}{2}$）x，（-1≤x≤0）的值域为B．
    （1）求A∩B；
    （2）若C={x|a≤x≤2a-1}，且C∩B=C，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．“|x|＜2”是“x2-x-6＜0”的（　　）
    A．既不充分也不必要条件B．必要不充分条件
    C．充要条件D．充分而不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．两圆x2+y2-1=0与x2+y2+3x+9y+2=0的公共弦长为（　　）
    A．$\frac{{3\sqrt{10}}}{10}$B．$\frac{{3\sqrt{10}}}{5}$C．$\frac{{\sqrt{10}}}{5}$D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

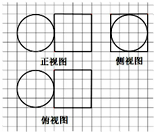
    9．如图，小方格是边长为1的正方形，一个几何体的三视图如图，则原几何体的体积为（　　）
    A．$\frac{32π}{3}$B．64+$\frac{32π}{3}$C．16πD．64+$\frac{256π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．数列{an}前n项和为Sn，且an+Sn=-2n-1（n∈N*）．
    （1）证明数列{an+2}为等比数列；
    （2）求数列{an}的通项公式；
    （3）若${b_n}={log_2}\frac{1}{{{a_n}+2}}$，证明：$\sum_{k=1}^n{\frac{1}{{{b_k}{b_{k+1}}}}}＜1$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．函数f（x）=$\frac{{2sin\frac{x}{2}cos\frac{x}{2}-1}}{{\sqrt{3-2cosx-4sin\frac{x}{2}cos\frac{x}{2}}}}$（0≤x≤2π）的值域是 （　　）
    A．[-$\frac{{\sqrt{2}}}{2}，0$]B．[-1，0]C．[-$\sqrt{2}，0$]D．[-$\sqrt{3}，0$]

    查看答案和解析>>

    同步练习册答案