
【题目】![]() 是等边三角形,边长为4,
是等边三角形,边长为4, ![]() 边的中点为
边的中点为![]() ,椭圆
,椭圆![]() 以
以![]() ,
, ![]() 为左、右两焦点,且经过
为左、右两焦点,且经过![]() 、
、![]() 两点。
两点。
(1)求该椭圆的标准方程;
(2)过点![]() 且
且![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点,求证:直线
两点,求证:直线![]() 与
与![]() 的交点在一条定直线上.
的交点在一条定直线上.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的上下两个焦点分别为
的上下两个焦点分别为![]() ,
, ![]() ,过点
,过点![]() 与
与![]() 轴垂直的直线交椭圆
轴垂直的直线交椭圆![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 的面积为
的面积为![]() ,椭圆
,椭圆![]() 的离心力为
的离心力为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知![]() 为坐标原点,直线
为坐标原点,直线![]() :
: ![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() ,
, ![]() 两个不同的点,若存在实数
两个不同的点,若存在实数![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市需对某环城快速车道进行限速,为了调研该道路车速情况,于某个时段随机对![]() 辆车的速度进行取样,测量的车速制成如下条形图:
辆车的速度进行取样,测量的车速制成如下条形图:
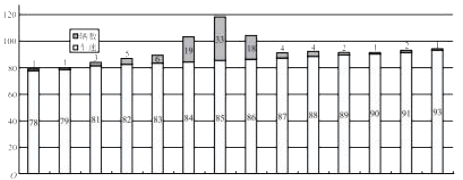
经计算:样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.已知车速过慢与过快都被认为是需矫正速度,现规定车速小于
,以频率值作为概率的估计值.已知车速过慢与过快都被认为是需矫正速度,现规定车速小于![]() 或车速大于
或车速大于![]() 是需矫正速度.
是需矫正速度.
(1)从该快速车道上所有车辆中任取![]() 个,求该车辆是需矫正速度的概率;
个,求该车辆是需矫正速度的概率;
(2)从样本中任取![]() 个车辆,求这
个车辆,求这![]() 个车辆均是需矫正速度的概率;
个车辆均是需矫正速度的概率;
(3)从该快速车道上所有车辆中任取![]() 个,记其中是需矫正速度的个数为
个,记其中是需矫正速度的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为14分)已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人为了响应政府“节能减排”的号召,决定各购置一辆纯电动汽车.经了解目前市场上销售的主流纯电动汽车,按续驶里程数![]() (单位:公里)可分为三类车型,
(单位:公里)可分为三类车型, ![]() ,
, ![]() .甲从
.甲从![]() 三类车型中挑选,乙从
三类车型中挑选,乙从![]() 两类车型中挑选,甲、乙两人选择各类车型的概率如表:
两类车型中挑选,甲、乙两人选择各类车型的概率如表:
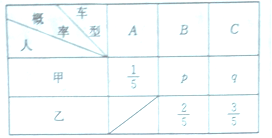
已知甲、乙都选![]() 类型的概率为
类型的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)求甲、乙选择不同车型的概率;
(3)某市对购买纯电动汽车进行补贴,补贴标准如下表:

记甲、乙两人购车所获得的财政补贴之和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一张长为![]() ,宽为
,宽为![]() (
(![]() )的长方形铁皮
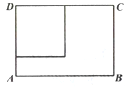
)的长方形铁皮![]() ,准备用它做成一个无盖长方体铁皮容器,要求材料利用率为100%,不考虑焊接处损失.如图,在长方形
,准备用它做成一个无盖长方体铁皮容器,要求材料利用率为100%,不考虑焊接处损失.如图,在长方形![]() 的一个角上剪下一块边长为
的一个角上剪下一块边长为![]() 的正方形铁皮,作为铁皮容器的底面,用余下材料剪拼后作为铁皮容器的侧面,设长方体的高为
的正方形铁皮,作为铁皮容器的底面,用余下材料剪拼后作为铁皮容器的侧面,设长方体的高为![]() ,体积为
,体积为![]() .
.
(Ⅰ)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)求该铁皮容器体积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某商品的进货单价为1元/件,商户甲往年以单价2元/件销售该商品时,年销量为1万件.今年拟下调销售单价以提高销量增加收益.据估算,若今年的实际销售单价为![]() 元/件(
元/件(![]() ),则新增的年销量
),则新增的年销量![]() (万件).
(万件).
(1)写出今年商户甲的收益![]() (单位:万元)与
(单位:万元)与![]() 的函数关系式;
的函数关系式;
(2)商户甲今年采取降低单价提高销量的营销策略,是否能获得比往年更大的收益(即比往年收益更多)?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com