
【题目】已知圆心在y轴上的圆C经过点A(1,2)和点B(0,3).
(Ⅰ)求圆C的方程;
(Ⅱ)若直线l在两坐标轴上的截距相等,且被圆C截得的弦长为 ![]() ,求l的方程.
,求l的方程.
【答案】解:(Ⅰ)由已知,得线段AB的中点坐标为( ![]() ,
, ![]() ),
),
直线AB的斜率kAB= ![]() =﹣1,
=﹣1,
所以线段AB的垂直平分线的方程为y﹣ ![]() =x﹣
=x﹣ ![]() ,即x﹣y+2=0.
,即x﹣y+2=0.
由题意,圆C的圆心C在直线x﹣y+2=0上,又在y轴上,所以C(0,2),
半径r=|BC|=1,所以圆C的方程为x2+(y﹣2)2=1. ….(6分)
(Ⅱ)由题意,直线不过原点,设方程为x+y﹣a=0,
∵直线被圆C截得的弦长为 ![]() ,
,
∴圆心到直线的距离为 ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴a=1或3,
∴所求直线方程为x+y﹣1=0或x+y﹣3=0,
直线过原点,设直线l的方程为y=kx.∴ ![]() =
= ![]() ,
,
∴k= ![]() x,∴所求直线方程为y=
x,∴所求直线方程为y= ![]() x.
x.
综上所述所求直线为x+y﹣1=0或x+y﹣3=0或y= ![]() x
x
【解析】(Ⅰ)求出线段AB的垂直平分线的方程,结合圆C的圆心C在直线x﹣y+2=0上,又在y轴上,求出圆心坐标与半径,即可求圆C的方程;
(Ⅱ)由题意,分类讨论,设方程,利用直线被圆C截得的弦长为 ![]() ,可得圆心到直线的距离为
,可得圆心到直线的距离为 ![]() ,即可求出直线的方程.
,即可求出直线的方程.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos(ωx+α)(A>0,ω>0,0<α<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为 . 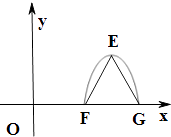
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y=sin2x的图象,可由函数 ![]() ( )
( )
A.向左平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向右平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,A(1,1),B(2,0),| ![]() |=1.
|=1.
(1)求 ![]() 与
与 ![]() 夹角;
夹角;
(2)若 ![]() 与
与 ![]() 垂直,求点C的坐标;
垂直,求点C的坐标;
(3)求| ![]() +
+ ![]() +
+ ![]() |的取值范围.
|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信运动和运动手环的普及,增强了人民运动的积极性,每天一万步称为一种健康时尚,某中学在全校范围内内积极倡导和督促师生开展“每天一万步”活动,经过几个月的扎实落地工作后,学校想了解全校师生每天一万步的情况,学校界定一人一天走路不足![]() 千步为不健康生活方式,不少于
千步为不健康生活方式,不少于![]() 千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为
千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为![]() 人,高一学生人数为
人,高一学生人数为![]() 人,高二学生人数
人,高二学生人数![]() 人,高三学生人数
人,高三学生人数![]() ,从中抽取
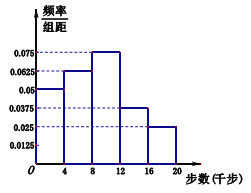
,从中抽取![]() 人作为调查对象,得到了如图所示的这
人作为调查对象,得到了如图所示的这![]() 人的频率分布直方图,这
人的频率分布直方图,这![]() 人中有
人中有![]() 人被学校界定为不健康生活方式者.
人被学校界定为不健康生活方式者.
(1)求这次作为抽样调查对象的教师人数;
(2)根据频率分布直方图估算全校师生每人一天走路步数的中位数(四舍五入精确到整数步);
(3)校办公室欲从全校师生中速记抽取![]() 人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励
人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励![]() 元,超健康生活方式者表彰奖励
元,超健康生活方式者表彰奖励![]() 元,一般生活方式者鼓励性奖励
元,一般生活方式者鼓励性奖励![]() 元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额恰好为
元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额恰好为![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验.为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.
分数 |
|
|
|
|
|
甲班频数 | 5 | 6 | 4 | 4 | 1 |
一般频数 | 1 | 3 | 6 | 5 | 5 |
(1)由以下统计数据填写下面![]() 列联表,并判断能否在犯错误的额概率不超过0.025的前提下认为“成绩优良与教学方式有关”?
列联表,并判断能否在犯错误的额概率不超过0.025的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
附:![]() ,其中
,其中![]() .
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核.在这8人中,记成绩不优良的乙班人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x|x+bx+c,给出下列4个命题:
①b=0,c>0时,方程f(x)=0只有一个实数根;
②c=0时,y=f(x)是奇函数;
③y=f(x)的图象关于点(0,c)对称;
④方程f(x)=0至多有2个不相等的实数根.
上述命题中的所有正确命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com