
分析 (1)由题意可得:$\left\{\begin{array}{l}{2=acos\frac{π}{3}}\\{\sqrt{3}=bsin\frac{π}{3}}\end{array}\right.$,解得a,b,即可得出椭圆的标准方程.
(2)A(ρ1,θ),B(ρ2,θ+$\frac{π}{2}$)是曲线C上的两点,可得${ρ}_{1}^{2}(\frac{co{s}^{2}θ}{16}+\frac{si{n}^{2}θ}{4})=1$,${ρ}_{2}^{2}(\frac{si{n}^{2}θ}{16}+\frac{co{s}^{2}θ}{4})=1$,化简整理即可得出.
解答 解:(1)由题意可得:$\left\{\begin{array}{l}{2=acos\frac{π}{3}}\\{\sqrt{3}=bsin\frac{π}{3}}\end{array}\right.$,解得a=4,b=2.
∴曲线C的普通方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}$=1.
(2)A(ρ1,θ),B(ρ2,θ+$\frac{π}{2}$)是曲线C上的两点,
可得直角坐标(ρ1cosθ,ρ1sinθ),(-ρ2sinθ,ρ2cosθ),
代入椭圆标准方程可得:${ρ}_{1}^{2}(\frac{co{s}^{2}θ}{16}+\frac{si{n}^{2}θ}{4})=1$,${ρ}_{2}^{2}(\frac{si{n}^{2}θ}{16}+\frac{co{s}^{2}θ}{4})=1$.
∴$\frac{1}{ρ_1^2}$+$\frac{1}{ρ_2^2}$=$\frac{co{s}^{2}θ+si{n}^{2}θ}{16}$+$\frac{si{n}^{2}θ+co{s}^{2}θ}{4}$=$\frac{1}{16}+\frac{1}{4}$=$\frac{5}{16}$.
点评 本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程,考查了推理能力与计算能力,属于中档题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
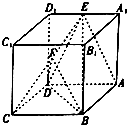 如图,正方体ABCD-A1B1C1D1中,AB=2,点E是A1D1的中点,点F是CE的中点.
如图,正方体ABCD-A1B1C1D1中,AB=2,点E是A1D1的中点,点F是CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥PB,PC=2.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥PB,PC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2-$\sqrt{2}$ | B. | 1 | C. | 2$\sqrt{2}$ | D. | 1+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{2},\frac{2}{3}}]$ | B. | $({\frac{2}{3},\frac{3}{4}}]$ | C. | $({\frac{3}{4},\frac{4}{5}}]$ | D. | $({\frac{4}{5},\frac{5}{6}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
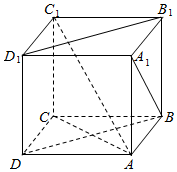 如图,对于正方体ABCD-A1B1C1D1,给出下列四个结论:
如图,对于正方体ABCD-A1B1C1D1,给出下列四个结论:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 120° | C. | 60°或120° | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com