
分析 (1)由题意知本题是一个超几何分步,随机变量X表示所选3人中女生的人数,X可能取的值为0,1,2,且$P({X=k})=\frac{{C_2^kC_4^{3-k}}}{C_6^3},k=0,1,2$,由此能求出X的分布列.
(2)由X的分布列能求出所选3人中最多有一名女生的概率.
解答 解:(1)由题意知本题是一个超几何分步,随机变量X表示所选3人中女生的人数,
X可能取的值为0,1,2,且$P({X=k})=\frac{{C_2^kC_4^{3-k}}}{C_6^3},k=0,1,2$,
P(X=0)=$\frac{{C}_{2}^{0}{C}_{4}^{3}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
P(X=1)=$\frac{{C}_{2}^{1}{C}_{4}^{2}}{{C}_{6}^{3}}$=$\frac{3}{5}$,
P(X=2)=$\frac{{C}_{2}^{2}{C}_{4}^{1}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列的求法,是中档题,解题时要认真审题,注意超几何分布的性质的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 共线向量的方向相同 | B. | 零向量是$\overrightarrow{0}$ | ||
| C. | 长度相等的向量叫做相等向量 | D. | 共线向量是在一条直线上的向量 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
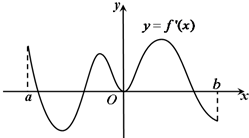 函数f(x)的导函数f′(x)在区间(a,b)内的图象如图所示,则f(x)在(a,b)内的极大值点有( )
函数f(x)的导函数f′(x)在区间(a,b)内的图象如图所示,则f(x)在(a,b)内的极大值点有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
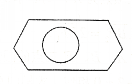 如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置可能性相等),恰有27粒落入半径为1的圆内,则该多边形的面积约为( )
如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置可能性相等),恰有27粒落入半径为1的圆内,则该多边形的面积约为( )| A. | 4π | B. | 5π | C. | 6π | D. | 7π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 棱台的侧面一定不会是平行四边形 | |
| B. | 棱锥的侧面只能是三角形 | |
| C. | 由四个面围成的封闭图形只能是三棱锥 | |
| D. | 棱锥被平面截成的两部分不可能都是棱锥 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com