
分析 利用分步乘法求出两同学总的选法种数,再求出选法相同的选法种数,利用古典概型概率计算公式得答案.
解答 解:甲同学从四种水果中选两种,选法种数为${C}_{4}^{2}$,乙同学的选法种数为${C}_{4}^{2}$,
则两同学的选法种数为${C}_{4}^{2}•{C}_{4}^{2}$种.
两同学相同的选法种数为${C}_{4}^{2}$.
由古典概型概率计算公式可得:甲、乙两同学各自所选的两种水果相同的概率为$\frac{{C}_{4}^{2}}{{C}_{4}^{2}•{C}_{4}^{2}}=\frac{1}{{C}_{4}^{2}}=\frac{1}{6}$.
故答案为:$\frac{1}{6}$.
点评 本题考查古典概型概率计算公式的应用,考查了组合及组合数公式,是基础题.


科目:高中数学 来源: 题型:选择题
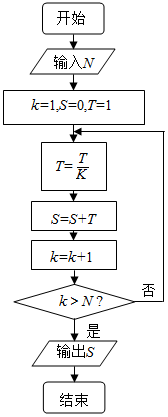
| A. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{10}$ | B. | $1+\frac{1}{2}+\frac{1}{3×2}+\frac{1}{2×3×4…×10}$ | ||
| C. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{11}$ | D. | $1+\frac{1}{2}+\frac{1}{2×3}+\frac{1}{2×3×4…×11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P((A1+A2)|$\overline{B}$)=P(A1|$\overline{B}$)+P(A2|$\overline{B}$) | B. | P(A1B+A2B)=P(A1B)+P(A2B) | ||
| C. | P(A1+A2)=P(A1|B)+P(A2|B) | D. | P(B)=P(A1)P(B|A1)+P(A2)P(B|A2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,$\widehat{AC}$长为$\frac{5π}{6}$,$\widehat{{A}_{1}{B}_{1}}$长为$\frac{π}{3}$,其中B1与C在平面AA1O1O的同侧.
将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,$\widehat{AC}$长为$\frac{5π}{6}$,$\widehat{{A}_{1}{B}_{1}}$长为$\frac{π}{3}$,其中B1与C在平面AA1O1O的同侧.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com