
| 1 |
| 5 |
| 4 |
| 5 |
| 3 |
| 10 |
|
| 3 |
| 10 |
|
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 10 |
| 1 |
| 2 |
| 4 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| 2500r |
| 5r+1 |
| 2500r |
| 5r+1 |
| 1 |
| 5 |
| 3 |
| 10 |


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:044
选菜问题:学校餐厅每天供应
500名学生用餐,每星期一有A、B两种菜可供选择.调查资料表明,凡是在这星期一选A种菜的,下星期一会有20%改选B种菜;而选B种菜的,下星期一会有30%改选A种菜.用 ,
, 分别表示在第n个星期选A的人数和选B的人数,如果
分别表示在第n个星期选A的人数和选B的人数,如果 ,求
,求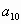 .
.查看答案和解析>>
科目:高中数学 来源: 题型:
学校餐厅每天供应500名学生用餐,每星期一有![]() 、
、![]() 两种菜可供选择.调查资料表明,凡是在这星期一选
两种菜可供选择.调查资料表明,凡是在这星期一选![]() 种菜的,下星期一会有
种菜的,下星期一会有![]() 改选
改选![]() 种菜;而选
种菜;而选![]() 种菜的,下星期一有
种菜的,下星期一有![]() 改选
改选![]() 种菜.用
种菜.用![]() ,
,![]() 分别表示在第
分别表示在第![]() 个星期选
个星期选![]() 的人数和选
的人数和选![]() 的人数,如果
的人数,如果![]() ,求
,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
学校餐厅每天有500名学生就餐,每星期一有A,B两种套餐可选,每个学生任选一种,其中A是本校的传统套餐,B是从外校引人的套餐.调查资料表明,若在这星期一选A套餐的学生,下星期一会有![]() 的学生改选B套餐;而选B套餐的学生,下周星期一会有
的学生改选B套餐;而选B套餐的学生,下周星期一会有![]() (
(![]() )的学生改选A套餐,用
)的学生改选A套餐,用![]() ,
,![]() 分别表示在第
分别表示在第![]() 个星期选A套餐的人数和选B套餐的人数.
个星期选A套餐的人数和选B套餐的人数.
(I)用![]() 表示
表示![]() ;
;
(II)若![]() ,且选A套餐的学生人数保持不变,求
,且选A套餐的学生人数保持不变,求![]() ;
;
(III)根据调查,存在一个常数![]() ,使得数列
,使得数列![]() 为等比数列,且
为等比数列,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com