
分析 (1)设长方体容器的高为h(h>0),依据题意知2xh=9,所以h=$\frac{9}{2x}$,从而写出该容器成本y(单位:元)表示成底面边长x(单位:米)的函数;
(2)利用基本不等式,即可得到所求的最值和对应的x的值.
解答 解:(1)设长方体容器的高为h(h>0),依据题意知2xh=9,所以h=$\frac{9}{2x}$,-------------3分
容器的侧面积为4h+2xh,容器底面积为2x,
所以y=4ax+a(4h+2xh)=2a(2x+$\frac{9}{x}$)+9a(x>0)-----------------------8分
(2)令f(x)=2x+$\frac{9}{x}$(x>0),所以2x+$\frac{9}{x}$≥6$\sqrt{2}$,-------------------------------------------10分
当且仅当2x=$\frac{9}{x}$,即x=$\frac{3\sqrt{2}}{2}$时,函数取得最小值.-------------------------------------------12分
答:当容器底面边长为$\frac{3\sqrt{2}}{2}$米时,其成本最低.-------------------------------------------14分
点评 本题考查了基本不等式在实际问题中的应用,考查数学建模思想的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
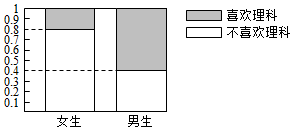
| A. | 性别与是否喜欢理科无关 | B. | 女生中喜欢理科的比为80% | ||
| C. | 男生比女生喜欢理科的可能性大 | D. | 男生中喜欢理科的比例为80% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
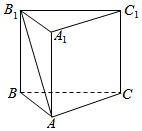 如图,直三棱柱ABC-A1B1C1的各条棱长均为4,D是侧棱CC1的中点.
如图,直三棱柱ABC-A1B1C1的各条棱长均为4,D是侧棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某隧道的截面图由矩形ABCD和抛物线型拱顶DEC组成(E为拱顶DEC的最高点),以AB所在直线为x轴,以AB的中点为坐标原点,建立平面直角坐标系xOy,已知拱顶DEC的方程为y=-$\frac{1}{4}$x2+6(-4≤x≤4).
如图,某隧道的截面图由矩形ABCD和抛物线型拱顶DEC组成(E为拱顶DEC的最高点),以AB所在直线为x轴,以AB的中点为坐标原点,建立平面直角坐标系xOy,已知拱顶DEC的方程为y=-$\frac{1}{4}$x2+6(-4≤x≤4).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
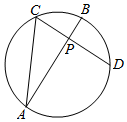 如图,AB、CD是⊙O的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=2$\sqrt{5}$,则线段AC的长度为( )
如图,AB、CD是⊙O的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=2$\sqrt{5}$,则线段AC的长度为( )| A. | 5 | B. | $\sqrt{35}$ | C. | $\sqrt{30}$ | D. | 3$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{2}$ | B. | 4 | C. | $\sqrt{3}$ | D. | 9$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com