
【题目】设a为非负实数,函数![]() .
.

(1)当![]() 时,画出函数
时,画出函数![]() 的草图,并写出函数
的草图,并写出函数![]() 的单调递增区间;
的单调递增区间;
(2)若函数![]() 有且只有一个零点,求实数a的取值范围.
有且只有一个零点,求实数a的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某民营企业生产A,B两种产品,根据市场调查与预测,A产品的利润y与投资x成正比,其关系如图甲,B产品的利润y与投资x的算术平方根成正比,其关系如图乙![]() 注:利润与投资单位为万元
注:利润与投资单位为万元![]()

![]() 分别将A,B两种产品的利润y表示为投资x的函数关系式;
分别将A,B两种产品的利润y表示为投资x的函数关系式;
![]() 该企业已筹集到10万元资金,并全部投入A,B两种产品的生产
该企业已筹集到10万元资金,并全部投入A,B两种产品的生产![]() 问:怎样分配这10万元资金,才能使企业获得最大利润,最大利润是多少万元?
问:怎样分配这10万元资金,才能使企业获得最大利润,最大利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组调查学生使用智能手机对学习成绩的影响,询问了30名同学,得到如下的![]() 列联表:
列联表:
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
(Ⅰ)根据以上![]() 列联表判断,能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响?
列联表判断,能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响?
(Ⅱ)从使用智能手机的20名同学中,按分层抽样的方法选出5名同学,求所抽取的5名同学中“学习成绩优秀”和“学习成绩不优秀”的人数;
(Ⅲ)从问题(Ⅱ)中被抽取的5名同学,再随机抽取3名同学,试求抽取3名同学中恰有2名同学为“学习成绩不优秀”的概率.
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】夏天喝冷饮料已成为年轻人的时尚. 某饮品店购进某种品牌冷饮料若干瓶,再保鲜.
(Ⅰ)饮品成本由进价成本和可变成本(运输、保鲜等其它费用)组成.根据统计,“可变成本”![]() (元)与饮品数量
(元)与饮品数量![]() (瓶)有关系.
(瓶)有关系.![]() 与
与![]() 之间对应数据如下表:
之间对应数据如下表:
饮品数量 | 2 | 4 | 5 | 6 | 8 |
可变成本 | 3 | 4 | 4 | 4 | 5 |
依据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;如果该店购入20瓶该品牌冷饮料,估计“可变成本”约为多少元?
;如果该店购入20瓶该品牌冷饮料,估计“可变成本”约为多少元?
(Ⅱ)该饮品店以每瓶10元的价格购入该品牌冷饮料若干瓶,再以每瓶15元的价格卖给顾客。如果当天前8小时卖不完,则通过促销以每瓶5元的价格卖给顾客(根据经验,当天能够把剩余冷饮料都低价处理完毕,且处理完毕后,当天不再购进).该店统计了去年同期100天该饮料在每天的前8小时内的销售量(单位:瓶),制成如下表:
每日前8个小时 销售量(单位:瓶) | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
频数 | 10 | 15 | 16 | 16 | 15 | 13 | 15 |
若以100天记录的频率作为每日前8小时销售量发生的概率,若当天购进18瓶,求当天利润的期望值.
(注:利润=销售额![]() 购入成本
购入成本![]() “可变本成”)
“可变本成”)
参考公式:回归直线方程为![]() ,其中
,其中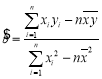
参考数据:![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人造地球卫星绕地球运行遵循开普勒行星运动定律:卫星在以地球为焦点的椭圆轨道上绕地球运行时,其运行速度是变化的,速度的变化服从面积守恒规律,即卫星的向径(卫星至地球的连线)在相同的时间内扫过的面积相等.设椭圆的长轴长、焦距分别为![]() 李明根据所学的椭圆知识,得到下列结论:
李明根据所学的椭圆知识,得到下列结论:

①卫星向径的最小值为![]() ,最大值为
,最大值为![]() ;
;
②卫星向径的最小值与最大值的比值越小,椭圆轨道越扁;
③卫星运行速度在近地点时最小,在远地点时最大
其中正确结论的个数是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水产试验厂实行某种鱼的人工孵化,10 000个鱼卵能孵化8 513尾鱼苗,根据概率的统计定义解答下列问题:
(1)这种鱼卵的孵化率(孵化概率)是多少?
(2)30 000个鱼卵大约能孵化多少尾鱼苗?
(3)要孵化5 000尾鱼苗,大概需要多少个鱼卵?(精确到百位)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com