
分析 (I)由数列{Sn}为单调递增数列及二次函数的性质可知-$\frac{λ}{2}$<$\frac{3}{2}$,从而解得;
(Ⅱ)分类讨论以求得an=2n-1+λ,再由a1+a4+a6+a9=40可得λ=1;从而解得an•2${\;}^{{a}_{n}}$=2n•22n=n•22n+1,从而利用错位相减法求其前n项和.
解答 解:(I)∵数列{Sn}满足:Sn=n2+λn(λ∈R),且为单调递增数列.
而二次函数y=x2+λx的图象对称轴为x=-$\frac{λ}{2}$,
故只需使对称轴在(1,2)中点值的左侧即可,
即-$\frac{λ}{2}$<$\frac{3}{2}$,
故λ>-3;
(Ⅱ)①当n=1时,a1=S1=1+λ,
②当n≥2时,an=Sn-Sn-1
=(n2+λn)-((n-1)2+λ(n-1))
=2n-1+λ,
a1=1+λ也满足an=2n-1+λ,
综上所述,数列{an}是以1+λ为首项,2为公差的等差数列;
且an=2n-1+λ,
又∵a1+a4+a6+a9=40,
∴a5=10,
即10-1+λ=10,
故λ=1;
故an=2n,
故an•2${\;}^{{a}_{n}}$=2n•22n=n•22n+1,
令数列{an•2${\;}^{{a}_{n}}$}的前n项和为Tn,
则Tn=1•23+2•25+3•27+…+n•22n+1,
4Tn=1•25+2•27+3•29+…+n•22n+3,
两式作差可得,
3Tn=-23-25-27-…-22n+1+n•22n+3=(n-$\frac{1}{3}$)22n+3+$\frac{8}{3}$,
故Tn=($\frac{n}{3}$-$\frac{1}{9}$)22n+3+$\frac{8}{9}$.
点评 本题考查了函数在数列中的应用及分类讨论的思想应用,同时考查了错位相减法的应用.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1-ln2}{4}$ | B. | $\frac{3-2ln2}{4}$ | C. | $\frac{1+ln2}{4}$ | D. | $\frac{1+2ln2}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{3}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
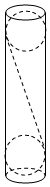 如图所示,一个圆乒乓球筒,高为20厘米,底面半径为2厘米,球桶的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计),一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
如图所示,一个圆乒乓球筒,高为20厘米,底面半径为2厘米,球桶的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计),一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )| A. | $\frac{1}{5}$ | B. | $\frac{\sqrt{15}}{4}$ | C. | $\frac{2\sqrt{6}}{5}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一定共线 | B. | 一定不共线 | C. | 可能共线 | D. | 可能不共线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com