
分析 先根据题意设出总销售量y,表示出y的表达式,利用等比数列的求和公式对数函数的性质求得n.
解答 解:设总销售量y,题意可知y=4000[1+(1+0.1)1+…+(1+0.1)n-1],
4000[1+(1+0.1)1+…+(1+0.1)n-1]=24000,
∴(1+0.1)0+(1+0.1)1+…+(1+0.1)n-1=6,
∴$\frac{1×(1-1.{1}^{n})}{1-1.1}$=6,
∴1.1n=1.6,
∴n=$\frac{lg1.6}{lg1.1}$≈5,
故大约5年可使总销售量达到24000台.
点评 本题主要考查了等比数列的通项公式和求和公式.解题的关键是根据题意表示出数列的通项公式.


科目:高中数学 来源: 题型:填空题
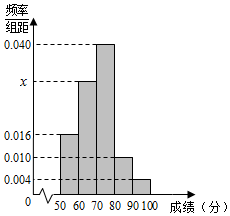 某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100]的有2人,由此推测频率分布直方图中的x=0.03.
某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100]的有2人,由此推测频率分布直方图中的x=0.03.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 是奇函数又是偶函数 | D. | 非奇函数非偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com