
| A. | $\frac{1-ln2}{4}$ | B. | $\frac{3-2ln2}{4}$ | C. | $\frac{1+ln2}{4}$ | D. | $\frac{1+2ln2}{4}$ |
分析 由题意画出图形,利用区域的面积比求概率.
解答 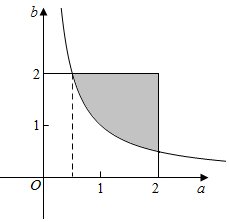 解:如图所示:使得函数f(x)=lg(ax2-2x+b)的值域为R的范围为$\left\{\begin{array}{l}{a>0}\\{△=4-4ab<0}\end{array}\right.$,即b>$\frac{1}{a}$,
解:如图所示:使得函数f(x)=lg(ax2-2x+b)的值域为R的范围为$\left\{\begin{array}{l}{a>0}\\{△=4-4ab<0}\end{array}\right.$,即b>$\frac{1}{a}$,
S矩形=2×2=4,
S=${∫}_{\frac{1}{2}}^{2}$$\frac{1}{a}$da=lna|${\;}_{\frac{1}{2}}^{2}$=ln2-ln$\frac{1}{2}$=2ln2
∴S阴影=$\frac{3}{2}×$2-2ln2=3-2ln2,
∴则使得函数f(x)=ln(ax2-2x+b)的值域为R的概率是$\frac{3-2ln2}{4}$,
故选:B.
点评 本题考查了几何概型的概率求法;关键是明确事件的测度,利用公式解答.


科目:高中数学 来源: 题型:解答题
 某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:
某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
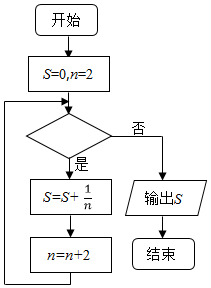
| A. | n=6 | B. | n<6 | C. | n≤6 | D. | n≤8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1<x1x2<$\sqrt{e}$ | B. | $\frac{1}{\sqrt{e}}$<x1x2<1 | C. | 2<x1x2<2$\sqrt{e}$ | D. | $\frac{2}{\sqrt{e}}$<x1x2<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (0,1) | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com