
分析 先求出公差d=-4,从而an=40-4n,a10=0,进而|Tn|取得最小值时的n的值为第10项的前3项或前2项,由此能求出n的值.
解答 解:∵{an}是等差数列,a6=16,a12=-8,
∴$d=\frac{{{a_{12}}-{a_6}}}{12-6}=-4$,
∴an=a6+(n-6)d=40-4n,a10=0,
∵数列{an}的第n项到第n+5项的和为连续6项的和,
∴|Tn|取得最小值时的n的值为第10项的前3项或前2项,
即n的值为7或8.
故答案为:7或8.
点评 本题考查等差数列的前n项和的绝对值最小时项数n的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 判断模型的拟合效果 | |
| B. | 对两个变量进行相关分析 | |
| C. | 给出两个分类变量有关系的可靠程度 | |
| D. | 估计预报变量的平均值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
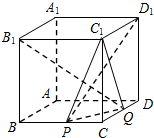 如图所示,在棱长为2的正方体AC1中,点P,Q分别在棱BC、CD上,满足B1Q⊥D1P,且PQ=$\sqrt{2}$.
如图所示,在棱长为2的正方体AC1中,点P,Q分别在棱BC、CD上,满足B1Q⊥D1P,且PQ=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com