
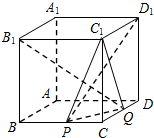
 如图所示,在棱长为2的正方体AC1中,点P,Q分别在棱BC、CD上,满足B1Q⊥D1P,且PQ=$\sqrt{2}$.
如图所示,在棱长为2的正方体AC1中,点P,Q分别在棱BC、CD上,满足B1Q⊥D1P,且PQ=$\sqrt{2}$.分析 (1)以 $\overrightarrow{AB}$、$\overrightarrow{AD}$、$\overrightarrow{A{A}_{1}}$为正交基底建立空间直角坐标系A-xyz,设CP=a(0≤a≤$\sqrt{2}$),利用 $\overrightarrow{{B}_{1}Q}$•$\overrightarrow{{D}_{1}P}$=0,得出关于a的方程并求解即可.
(2)分别求出$\overrightarrow{{B}_{1}Q}$、面APQ的一个法向量,利用两向量夹角可求cos<$\overrightarrow{{B}_{1}Q}$,$\overrightarrow{k}$>,即可得解.
解答 (本题满分为10分)
解:(1)以$\overrightarrow{AB}$、$\overrightarrow{AD}$、$\overrightarrow{A{A}_{1}}$为正交基底建立空间直角坐标系A-xyz,设CP=a(0≤a≤$\sqrt{2}$),
则CQ=$\sqrt{2-{a}^{2}}$,P(2,2-a,0),Q(2-$\sqrt{2-{a}^{2}}$,2,0),B1(2,0,2),D1(0,2,2),$\overrightarrow{{B}_{1}Q}$=(-$\sqrt{2-{a}^{2}}$,2,-2),$\overrightarrow{{D}_{1}P}$=(2,-a,-2),
∵B1Q⊥D1P,
∴$\overrightarrow{{B}_{1}Q}$•$\overrightarrow{{D}_{1}P}$=0,∴-$\sqrt{2-{a}^{2}}$-2a+4=0,
解得a=1,…(4分)
∴PC=1,CQ=1,即P、Q分别为BC,CD中点.…(5分)
(2)∵由(1)可得:$\overrightarrow{{B}_{1}Q}$=(-1,2,-2),$\overrightarrow{k}$=(0,0,-2)为面APQ的一个法向量,
∴cos<$\overrightarrow{{B}_{1}Q}$,$\overrightarrow{k}$>=$\frac{2}{3}$,
∴设B1Q与平面APQ所成角为θ,则sinθ=cos<$\overrightarrow{{B}_{1}Q}$,$\overrightarrow{k}$>=$\frac{2}{3}$…(10分)
点评 本题考查空间直线、平面位置关系的判断,二面角大小求解,考查空间想象能力、推理论证、计算、转化能力.利用向量这一工具,解决空间几何体问题,能够降低思维难度,属于中档题.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com