
分析 (Ⅰ)分离参数,构造函数,利用导数求出函数的最值,问题得以解决;
(Ⅱ)构造函数设$g(x)=\sqrt{e}x+\frac{{\sqrt{e}}}{2}-lnx(x>0)$,利用导数求出函数的最值,即可证明.
解答 解:(Ⅰ)∵$f(x)={e^x}-ax-\frac{a}{2}$,f(x)≥0在x∈R上恒成立,
∴a≤$\frac{{e}^{x}}{x+\frac{1}{2}}$,
设h(x)=$\frac{{e}^{x}}{x+\frac{1}{2}}$,
∴h′(x)=$\frac{{e}^{x}(x-\frac{1}{2})}{(x+\frac{1}{2})^{2}}$,
令h′(x)=0,解得x=$\frac{1}{2}$,
当x>$\frac{1}{2}$,即h′(x)>0,函数单调递增,
当x<$\frac{1}{2}$,即h′(x)<0,函数单调递减,
∴h(x)min=h($\frac{1}{2}$)=$\sqrt{e}$,
∴0<a≤$\sqrt{e}$,
故a的取值范围为$[0,\sqrt{e}]$;
(Ⅱ)设$g(x)=\sqrt{e}x+\frac{{\sqrt{e}}}{2}-lnx(x>0)$,
∴$g'(x)=\sqrt{e}-\frac{1}{x}(x>0)$,g'(x)>0,可得$x>\frac{1}{{\sqrt{e}}}$;g'(x)<0,可得$0<x<\frac{1}{{\sqrt{e}}}$.
∴g(x)在($\frac{1}{\sqrt{e}}$,+∞)上单调递增;在$(0,\frac{1}{{\sqrt{e}}})$上单调递减.
∴g(x)≥g($\frac{1}{\sqrt{e}}$)=$\frac{3+\sqrt{e}}{2}$,
∵$\sqrt{e}=1.64872…$,
∴$\sqrt{e}$>1.6,
∴g(x)>2.3.
由(Ⅰ)可得ex>$\sqrt{e}$x+$\frac{\sqrt{e}}{2}$,
∴ex-lnx的最小值大于2.3,
故若ex≥lnx+m对任意x>0恒成立,则m的最大值一定大于2.3.
点评 本题考查了导数和函数的最值的关系,关键是构造函数,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 判断模型的拟合效果 | |
| B. | 对两个变量进行相关分析 | |
| C. | 给出两个分类变量有关系的可靠程度 | |
| D. | 估计预报变量的平均值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
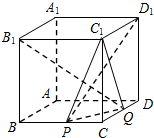 如图所示,在棱长为2的正方体AC1中,点P,Q分别在棱BC、CD上,满足B1Q⊥D1P,且PQ=$\sqrt{2}$.
如图所示,在棱长为2的正方体AC1中,点P,Q分别在棱BC、CD上,满足B1Q⊥D1P,且PQ=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com