
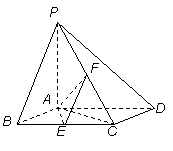
如图,已知四棱锥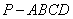 ,底面
,底面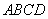 为菱形,
为菱形,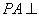 平面
平面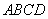 ,
,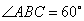 ,
,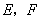 分别是
分别是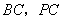 的中点.
的中点.
(1)证明: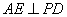 ;
;
 (2)若
(2)若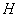 为
为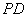 上的动点,
上的动点,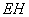 与平面
与平面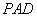 所成最大角的正弦值为
所成最大角的正弦值为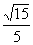 ,求二面角
,求二面角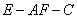 的余弦值.
的余弦值.
(1)证明:由四边形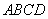 为菱形,
为菱形,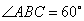 ,可得
,可得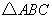 为正三角形.
为正三角形.
因为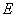 为
为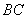 的中点,所以
的中点,所以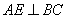
又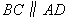 ,因此
,因此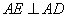
因为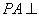 平面
平面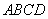 ,
,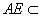 平面
平面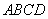 ,所以
,所以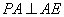
而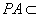 平面
平面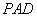 ,
, 平面
平面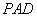 且
且
 所以
所以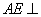 平面
平面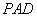 .又
.又 平面
平面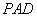
所以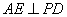 .------------------------------(3分)
.------------------------------(3分)
(2)解:设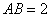 ,
,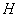 为
为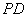 上任意一点,连接
上任意一点,连接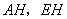 .
.
由(1)知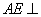 平面
平面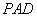
所以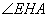 为
为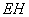 与平面
与平面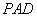 所成的角
所成的角
在 中,
中,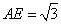 ,
,
所以当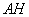 最短时,
最短时,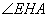 最大,即当
最大,即当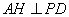 时,
时,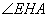 最大.
最大.
因为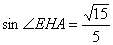 ,此时
,此时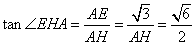
因此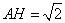 .又
.又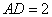 ,所以
,所以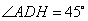 ,所以
,所以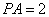 .----------------(5分)
.----------------(5分)
解法一:因为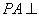 平面
平面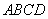 ,
,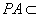 平面
平面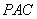
所以平面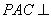 平面
平面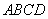
过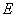 作
作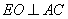 于
于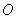 ,则
,则 平面
平面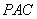
过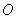 作
作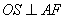 于
于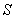 ,连接
,连接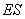 ,则
,则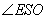 为二面角
为二面角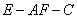 的平面角-------(7分)
的平面角-------(7分)
在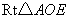 中,
中,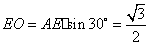 ,
,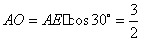
又 是
是 的中点,在
的中点,在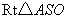 中,
中,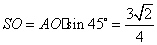
又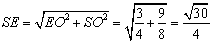
在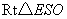 中,
中,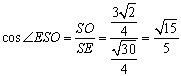 -------------------------------(9分)
-------------------------------(9分)
即所求二面角的余弦值为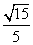 .-------------------------------------------(10分)
.-------------------------------------------(10分)
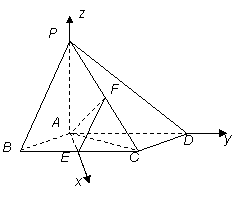
解法二:由(1)知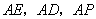 两两垂直,以
两两垂直,以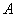 为坐标原点,建立如图所示的空间直角坐标系,又
为坐标原点,建立如图所示的空间直角坐标系,又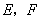 分别为
分别为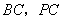 的中点,所以
的中点,所以
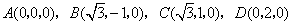
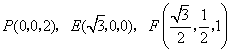
所以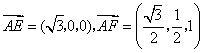
设平面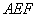 的一法向量为
的一法向量为
则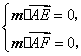 因此
因此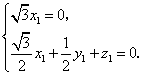
取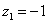 ,则
,则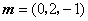 -----------------------------------------------(7分)
-----------------------------------------------(7分)
因为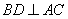 ,
,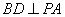 ,
,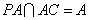 ,所以
,所以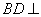 平面
平面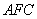
故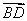 为平面
为平面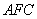 的一法向量,又
的一法向量,又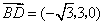
所以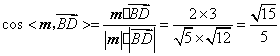 .---------------------------(9分)
.---------------------------(9分)
因为二面角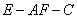 为锐角,所以所求二面角的余弦值为
为锐角,所以所求二面角的余弦值为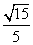 .-------------(10分)
.-------------(10分)
解法三:建立如图所示的空间直角坐标系,设菱形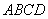 的边长为2,则
的边长为2,则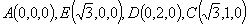 ,设
,设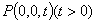
由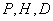 三点共线可设
三点共线可设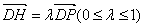 ,则
,则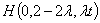 -------------(4分)
-------------(4分)
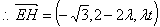 ,又平面
,又平面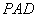 的一个法向量
的一个法向量
设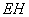 与平面
与平面 所成角为
所成角为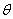 ,则
,则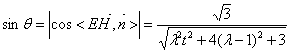 -(5分)
-(5分)
令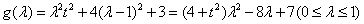
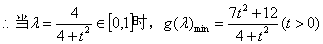 ---------------------------(6分)
---------------------------(6分)
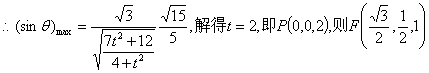 ------------(7分)
------------(7分)
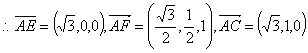
易得平面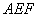 的一个法向量
的一个法向量 ;平面
;平面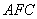 的一个法向量
的一个法向量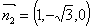 -(8分)
-(8分)
 ------------------------------------------(9分)
------------------------------------------(9分)
又 二面角
二面角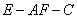 是锐二面角
是锐二面角
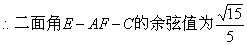


科目:高中数学 来源: 题型:
某地区有小学150所,中学75所,大学25所。现采用分层抽样的方法从这些学校中抽取60所学校对学生进行视力调查,应从小学中抽取 所学校,中学中抽取 所学校.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com