
分析 (Ⅰ)由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由特殊点的坐标求出φ的值,解直角三角形求出A,可得f(x)的解析式.
(Ⅱ)利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再利用正弦函数的单调性求得函数g(x)的单调递减区间.
解答 解:(Ⅰ)∵函数f(x)=Msin(ωx+φ)(M>0,ω>0,|φ|<$\frac{π}{2}$)的图象与x轴的两个相邻交点是A(0,0),B(6,0),
∴sinφ=0,∴φ=0,且$\frac{T}{2}$=$\frac{1}{2}•\frac{2π}{ω}$=6,∴ω=$\frac{π}{6}$,∴f(x)=Msin($\frac{π}{6}$x).
∵C是函数f(x)图象的一个最高点,a,b,c分别为△ABC的三个内角A,B,C的对边,
满足(a+c)(sinC-sinA)=(a+b)sinB,∴(a+c)(c-a)=(a+b)b,
整理可得$\frac{{a}^{2}{+b}^{2}{-c}^{2}}{2ab}$=-$\frac{1}{2}$,
即cosC=-$\frac{1}{2}$,∴C=$\frac{2π}{3}$.
由题意可得CA=CB,∴∠A=$\frac{π}{6}$,设AB的中点为D,则CD⊥AB,且点D(3,0),点C(3,M),
根据tan∠A=tan$\frac{π}{6}$=$\frac{\sqrt{3}}{3}$=$\frac{CD}{AD}$=$\frac{M}{3}$,∴M=$\sqrt{3}$,∴f(x)=$\sqrt{3}$sin($\frac{π}{6}$x).
(Ⅱ)将函数f(x)=$\sqrt{3}$sin($\frac{π}{6}$x)的图象向左平移1个单位后,纵坐标不变,
可得y=$\sqrt{3}$sin$\frac{π}{6}$(x+1)=$\sqrt{3}$sin($\frac{π}{6}$x+$\frac{π}{6}$)的图象;
再把横坐标伸长为原来的$\frac{π}{3}$倍,
得到函数g(x)=$\sqrt{3}$sin($\frac{3}{π}$•$\frac{π}{6}$x+$\frac{π}{6}$)=$\sqrt{3}$sin($\frac{1}{2}$x+$\frac{π}{6}$)的图象.
令2kπ+$\frac{π}{2}$≤$\frac{x}{2}$+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,求得4kπ+$\frac{2π}{3}$≤x≤4kπ+$\frac{8π}{3}$,
故函数g(x)的单调递减区间为[4kπ+$\frac{2π}{3}$,4kπ+$\frac{8π}{3}$],k∈Z.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由特殊点的坐标求出φ的值,解直角三角形求出A.还考查了函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ? | B. | 0 | C. | {0} | D. | {-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|1<x<3} | C. | {x|2<x<3} | D. | {x|x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
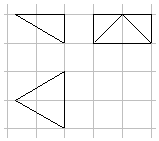 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是( )| A. | $\frac{19π}{3}$ | B. | $\frac{22π}{3}$ | C. | 19π | D. | 22π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 13 | C. | 4或10 | D. | 1或13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 对服务满意 | 对服务不满意 | 合计 | |
| 对商品满意 | 80 | ||
| 对商品不满意 | |||
| 合计 | 200 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com