
【题目】已知函数f(x)![]() ax﹣lnx(a∈R).
ax﹣lnx(a∈R).
(1)若a=2时,求函数f(x)的单调区间;
(2)设g(x)=f(x)![]() 1,若函数g(x)在
1,若函数g(x)在![]() 上有两个零点,求实数a的取值范围.
上有两个零点,求实数a的取值范围.
【答案】(1)单调递减区间为(0,![]() 1),单调递增区间为(
1),单调递增区间为(![]() 1,+∞)(2)(3,2e]
1,+∞)(2)(3,2e]
【解析】
(1)当a=2时,求出![]() ,求解
,求解![]() ,即可得出结论;
,即可得出结论;
(2)函数![]() 在
在![]() 上有两个零点等价于a=2x
上有两个零点等价于a=2x![]() 在
在![]() 上有两解,构造函数
上有两解,构造函数![]() ,
,![]() ,利用导数,可分析求得实数a的取值范围.
,利用导数,可分析求得实数a的取值范围.
(1)当a=2时,![]() 定义域为
定义域为![]() ,
,
则![]() ,令
,令![]() ,
,
解得x![]() 1,或x
1,或x![]() 1(舍去),
1(舍去),
所以当![]() 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 单调递增;
单调递增;
故函数的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,
,
(2)设![]() ,
,
函数g(x)在![]() 上有两个零点等价于
上有两个零点等价于![]() 在
在![]() 上有两解
上有两解
令![]() ,
,![]() ,则
,则![]() ,
,
令![]() ,
,![]() ,
,
显然,![]() 在区间
在区间![]() 上单调递增,又
上单调递增,又![]() ,
,
所以当![]() 时,有
时,有![]() ,即
,即![]() ,
,
当![]() 时,有
时,有![]() ,即
,即![]() ,
,
所以![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
![]() 时,
时,![]() 取得极小值,也是最小值,
取得极小值,也是最小值,
即![]() ,
,
由方程![]() 在
在![]() 上有两解及
上有两解及![]() ,
,
可得实数a的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】(多选)已知函数![]() ,其中正确结论的是( )
,其中正确结论的是( )
A.当![]() 时,函数
时,函数![]() 有最大值.
有最大值.
B.对于任意的![]() ,函数
,函数![]() 一定存在最小值.
一定存在最小值.
C.对于任意的![]() ,函数
,函数![]() 是
是![]() 上的增函数.
上的增函数.
D.对于任意的![]() ,都有函数
,都有函数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,已知每售出一箱酸奶的利润为50元,当天未售出的酸奶降价处理,以每箱亏损10元的价格全部处理完.若供不应求,可从其它商店调拨,每销售1箱可获利30元.假设该超市每天的进货量为14箱,超市的日利润为y元.为确定以后的订购计划,统计了最近50天销售该酸奶的市场日需求量,其频率分布表如图所示.
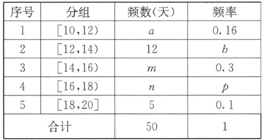
(1)求![]() 的值;
的值;
(2)求y关于日需求量![]() 的函数表达式;
的函数表达式;
(3)以50天记录的酸奶需求量的频率作为酸奶需求量发生的概率,估计日利润在区间[580,760]内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() ,圆
,圆![]() :
:![]() 与
与![]() 轴的正半轴的交点是
轴的正半轴的交点是![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() .
.

(1)若直线![]() 与
与![]() 轴交于
轴交于![]() ,且
,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线![]() ,
,![]() 的斜率分别是
的斜率分别是![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)设![]() 的中点为
的中点为![]() ,点
,点![]() ,若
,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且b(a2+c2﹣b2)=a2ccosC+ac2cosA.
(1)求角B的大小;
(2)若△ABC外接圆的半径为![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,E是棱
中,E是棱![]() 的中点,F是侧面
的中点,F是侧面![]() 内的动点,且
内的动点,且![]() 与平面
与平面![]() 的垂线垂直,如图所示,下列说法不正确的是( )
的垂线垂直,如图所示,下列说法不正确的是( )
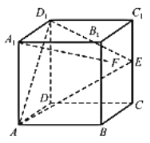
A.点F的轨迹是一条线段B.![]() 与BE是异面直线
与BE是异面直线
C.![]() 与
与![]() 不可能平行D.三棱锥
不可能平行D.三棱锥![]() 的体积为定值
的体积为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (其中
(其中![]() ,
,![]() 为自然对数的底数).
为自然对数的底数).
①![]() ,使得直线
,使得直线![]() 为函数
为函数![]() 的一条切线;
的一条切线;
②对![]() ,函数
,函数![]() 的导函数
的导函数![]() 无零点;
无零点;
③对![]() ,函数
,函数![]() 总存在零点;
总存在零点;
则上述结论正确的是______.(写出所有正确的结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
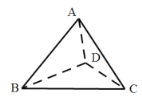
【题目】已知平面四边形![]() 中,
中,![]() ,
,![]() ,再将
,再将![]() 沿着
沿着![]() 翻折成三棱锥
翻折成三棱锥![]() 的过程中,直线
的过程中,直线![]() 与平面
与平面![]() 所成角均小于直线
所成角均小于直线![]() 与平面
与平面![]() 所成角,设二面角
所成角,设二面角![]() ,
,![]() 的大小分别为
的大小分别为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.存在
C.存在![]() D.存在
D.存在![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com