
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且b(a2+c2﹣b2)=a2ccosC+ac2cosA.
(1)求角B的大小;
(2)若△ABC外接圆的半径为![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
【答案】(1)B![]() (2)
(2)![]()
【解析】
(1)由已知结合余弦定理,正弦定理及和两角和的正弦公式进行化简可求cosB,进而可求B;
(2)由已知结合正弦定理,余弦定理及基本不等式即可求解ac的范围,然后结合三角形的面积公式即可求解.
(1)因为b(a2+c2﹣b2)=ca2cosC+ac2cosA,
∴![]() ,即2bcosB=acosC+ccosA
,即2bcosB=acosC+ccosA
由正弦定理可得,2sinBcosB=sinAcosC+sinCcosA=sin(A+C)=sinB,
因为![]() ,
,![]() 所以
所以![]() ,
,
所以B![]() ;
;
(2)由正弦定理可得,b=2RsinB![]() 2,
2,
由余弦定理可得,b2=a2+c2﹣2accosB,
即a2+c2﹣ac=4,因为a2+c2≥2ac,
所以4=a2+c2﹣ac≥ac,当且仅当a=c时取等号,即ac的最大值4,
所以△ABC面积S![]() 即面积的最大值
即面积的最大值![]() .
.


科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,
,![]() 单调递增,
单调递增,![]() ,若对任意
,若对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 在
在![]() 上的“追逐函数”.若
上的“追逐函数”.若![]() ,则下列四个命题:①
,则下列四个命题:①![]() 是
是![]() 在
在![]() 上的“追逐函数”;②若
上的“追逐函数”;②若![]() 是
是![]() 在
在![]() 上的“追逐函数”,则
上的“追逐函数”,则![]() ;③
;③![]() 是
是![]() 在
在![]() 上的“追逐函数”;④当
上的“追逐函数”;④当![]() 时,存在
时,存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“追逐函数”.其中正确命题的个数为( )
上的“追逐函数”.其中正确命题的个数为( )
A. ①③B. ②④C. ①④D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是![]() 年我国就业人口及劳动年龄人口(劳动年龄人口包含就业人口)统计表:
年我国就业人口及劳动年龄人口(劳动年龄人口包含就业人口)统计表:
时间(年) |
|
|
|
|
|
|
|
就业人口(万人) |
|
|
|
|
|
|
|
劳动年龄人口(万人) |
|
|
|
|
|
|
|
则由表可知( )
A.![]() 年我国就业人口逐年减少
年我国就业人口逐年减少
B.![]() 年我国劳动年龄人口逐年增加
年我国劳动年龄人口逐年增加
C.![]() 年这
年这![]() 年我国就业人口数量的中位数为
年我国就业人口数量的中位数为![]()
D.![]() 年我国劳动年龄人口中就业人口所占比重逐年增加
年我国劳动年龄人口中就业人口所占比重逐年增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为2的正方形.

(1)证明:A1C1![]() 平面ACD1;
平面ACD1;
(2)求异面直线CD与AD1所成角的大小;
(3)已知三棱锥D1﹣ACD的体积为![]() ,求AA1的长.
,求AA1的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调研高中生的作文水平.在某市普通高中的某次联考中,参考的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() 的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中
的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中![]() 构成以2为公比的等比数列.
构成以2为公比的等比数列.
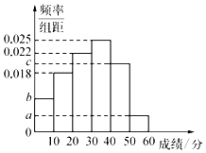
(1)求![]() 的值;
的值;
(2)填写下面![]() 列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
文科生 | 理科生 | 合计 | |
获奖 | 6 | ||
不获奖 | |||
合计 | 400 |
(3)将上述调查所得的频率视为概率,现从全市参考学生中,任意抽取2名学生,记“获得优秀作文”的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: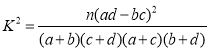 ,其中
,其中![]() .
.
| .15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() ax﹣lnx(a∈R).
ax﹣lnx(a∈R).
(1)若a=2时,求函数f(x)的单调区间;
(2)设g(x)=f(x)![]() 1,若函数g(x)在
1,若函数g(x)在![]() 上有两个零点,求实数a的取值范围.
上有两个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆C的标准方程;
(2)点P是椭圆上异于短轴端点A,B的任意一点,过点P作![]() 轴于Q,线段PQ的中点为M.直线AM与直线
轴于Q,线段PQ的中点为M.直线AM与直线![]() 交于点N,D为线段BN的中点,设O为坐标原点,试判断以OD为直径的圆与点M的位置关系.
交于点N,D为线段BN的中点,设O为坐标原点,试判断以OD为直径的圆与点M的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 中有一题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马,”马主曰:“我马食半牛”,今欲衰偿之,问各出几何?其意:今有牛、马、羊吃了别人的禾苗,苗主人要求赔偿五斗粟,羊主人说:“我羊所吃的禾苗只有马的一半”马主人说:“我马所吃的禾苗只有牛的一半”打算按此比例偿还,问羊的主人应赔偿______斗粟,在这个问题中牛主人比羊主人多赔偿______斗粟.
中有一题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马,”马主曰:“我马食半牛”,今欲衰偿之,问各出几何?其意:今有牛、马、羊吃了别人的禾苗,苗主人要求赔偿五斗粟,羊主人说:“我羊所吃的禾苗只有马的一半”马主人说:“我马所吃的禾苗只有牛的一半”打算按此比例偿还,问羊的主人应赔偿______斗粟,在这个问题中牛主人比羊主人多赔偿______斗粟.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数),其中
为自然对数的底数),其中![]() .
.
(1)在区间![]() 上,
上,![]() 是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
(2)若函数![]() 的两个极值点为
的两个极值点为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com