
【题目】下表是![]() 年我国就业人口及劳动年龄人口(劳动年龄人口包含就业人口)统计表:
年我国就业人口及劳动年龄人口(劳动年龄人口包含就业人口)统计表:
时间(年) |
|
|
|
|
|
|
|
就业人口(万人) |
|
|
|
|
|
|
|
劳动年龄人口(万人) |
|
|
|
|
|
|
|
则由表可知( )
A.![]() 年我国就业人口逐年减少
年我国就业人口逐年减少
B.![]() 年我国劳动年龄人口逐年增加
年我国劳动年龄人口逐年增加
C.![]() 年这
年这![]() 年我国就业人口数量的中位数为
年我国就业人口数量的中位数为![]()
D.![]() 年我国劳动年龄人口中就业人口所占比重逐年增加
年我国劳动年龄人口中就业人口所占比重逐年增加
 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
【题目】给出下列四个命题:①有的质数是偶数;②存在正整数![]() ,使得
,使得![]() 为
为![]() 的约数;③有的三角形三个内角成等差数列;④与给定的圆只有一个公共点的直线是圆的切线.其中既是存在性命题又是真命题的个数为( )
的约数;③有的三角形三个内角成等差数列;④与给定的圆只有一个公共点的直线是圆的切线.其中既是存在性命题又是真命题的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上、下、左、右四个顶点分别为
的上、下、左、右四个顶点分别为![]() x轴正半轴上的某点
x轴正半轴上的某点![]() 满足
满足![]() .
.
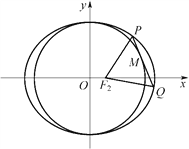
(1)求椭圆的方程;
(2)设该椭圆的左、右焦点分别为![]() ,点
,点![]() 在圆
在圆![]() 上,且
上,且![]() 在第一象限,过
在第一象限,过![]() 作圆
作圆![]() 的切线交椭圆于
的切线交椭圆于![]() ,求证:△
,求证:△![]() 的周长是定值.
的周长是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,已知每售出一箱酸奶的利润为50元,当天未售出的酸奶降价处理,以每箱亏损10元的价格全部处理完.若供不应求,可从其它商店调拨,每销售1箱可获利30元.假设该超市每天的进货量为14箱,超市的日利润为y元.为确定以后的订购计划,统计了最近50天销售该酸奶的市场日需求量,其频率分布表如图所示.
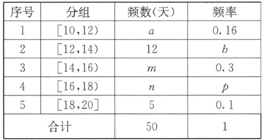
(1)求![]() 的值;
的值;
(2)求y关于日需求量![]() 的函数表达式;
的函数表达式;
(3)以50天记录的酸奶需求量的频率作为酸奶需求量发生的概率,估计日利润在区间[580,760]内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且b(a2+c2﹣b2)=a2ccosC+ac2cosA.
(1)求角B的大小;
(2)若△ABC外接圆的半径为![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时期著名的数学家刘徽对推导特殊数列的求和公式很感兴趣,创造并发展了许多算法,展现了聪明才智.他在《九章算术》“盈不足”章的第19题的注文中给出了一个特殊数列的求和公式.这个题的大意是:一匹良马和一匹驽马由长安出发至齐地,长安与齐地相距3000里(1里=500米),良马第一天走193里,以后每天比前一天多走13里.驽马第一天走97里,以后每天比前一天少走半里.良马先到齐地后,马上返回长安迎驽马,问两匹马在第几天相遇( )
A. 14天B. 15天C. 16天D. 17天
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com