
【题目】如图1,四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() 为
为![]() 的中点,以
的中点,以![]() 为折痕将
为折痕将![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,如图2.
,如图2.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由题意可证得![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,则平面
,则平面![]() 平面
平面![]() 可证;
可证;
(2)解法一:利用等体积法由![]() 可求出点
可求出点![]() 到平面
到平面![]() 的距离;解法二:由条件知点
的距离;解法二:由条件知点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,过点
的距离,过点![]() 作
作![]() 的垂线,垂足
的垂线,垂足![]() ,证明
,证明![]() 平面
平面![]() ,计算出
,计算出![]() 即可.
即可.
解法一:(1)依题意知,因为![]() ,所以
,所以![]() .
.
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以![]() .
.
由已知,![]() 是等边三角形,且
是等边三角形,且![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.


(2)在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() .
.
由(1)知,![]() 平面
平面![]() ,且
,且![]() ,
,
所以三棱锥![]() 的体积
的体积![]() .
.
在![]() 中,
中,![]() ,
,![]() ,得
,得![]() ,
,
由(1)知,![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() ,
,
设点![]() 到平面
到平面![]() 的距离
的距离![]() ,
,
则三棱锥![]() 的体积
的体积![]() ,得
,得![]() .
.
解法二:(1)同解法一;
(2)因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
所以点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离.
的距离.
过点![]() 作
作![]() 的垂线,垂足
的垂线,垂足![]() ,即
,即![]() .
.
由(1)知,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
由(1)知,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,得
,得![]() .
.
又![]() ,所以
,所以![]() .
.
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】绝大部分人都有患呼吸系统疾病的经历,现在我们调查患呼吸系统疾病是否和所处环境有关.一共调查了![]() 人,患有呼吸系统疾病的
人,患有呼吸系统疾病的![]() 人,其中
人,其中![]() 人在室外工作,
人在室外工作,![]() 人在室内工作.没有患呼吸系统疾病的
人在室内工作.没有患呼吸系统疾病的![]() 人,其中
人,其中![]() 人在室外工作,
人在室外工作,![]() 人在室内工作.
人在室内工作.
(1)现采用分层抽样从室内工作的居民中抽取一个容量为![]() 的样本,将该样本看成一个总体,从中随机的抽取两人,求两人都有呼吸系统疾病的概率.
的样本,将该样本看成一个总体,从中随机的抽取两人,求两人都有呼吸系统疾病的概率.
(2)你能否在犯错误率不超过![]() 的前提下认为感染呼吸系统疾病与工作场所有关;
的前提下认为感染呼吸系统疾病与工作场所有关;
附表:
|
|
|
|
|
|
|
|
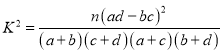
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,
,![]() 单调递增,
单调递增,![]() ,若对任意
,若对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 在
在![]() 上的“追逐函数”.若
上的“追逐函数”.若![]() ,则下列四个命题:①
,则下列四个命题:①![]() 是
是![]() 在
在![]() 上的“追逐函数”;②若
上的“追逐函数”;②若![]() 是
是![]() 在
在![]() 上的“追逐函数”,则
上的“追逐函数”,则![]() ;③
;③![]() 是
是![]() 在
在![]() 上的“追逐函数”;④当
上的“追逐函数”;④当![]() 时,存在
时,存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“追逐函数”.其中正确命题的个数为( )
上的“追逐函数”.其中正确命题的个数为( )
A. ①③B. ②④C. ①④D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任利用周末时间对该班级![]() 年最后一次月考的语文作文分数进行统计,发现分数都位于
年最后一次月考的语文作文分数进行统计,发现分数都位于![]() 之间,现将所有分数情况分为
之间,现将所有分数情况分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共七组,其频率分布直方图如图所示,已知
共七组,其频率分布直方图如图所示,已知![]() .
.

(1)求频率分布直方图中![]() 、
、![]() 的值;
的值;
(2)求该班级这次月考语文作文分数的平均数和中位数.(每组数据用该组区间中点值作为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.


(1)求频率分布直方图中![]() 的值;
的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解广大学生家长对校园食品安全的认识,某市食品安全检测部门对该市家长进行了一次校园食品安全网络知识问卷调查,每一位学生家长仅有一次参加机会,现对有效问卷进行整理,并随机抽取出了200份答卷,统计这些答卷的得分(满分:100分)制出的频率分布直方图如图所示,由频率分布直方图可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为这200人得分的平均值(同一组数据用该组区间的中点值作为代表).
近似为这200人得分的平均值(同一组数据用该组区间的中点值作为代表).
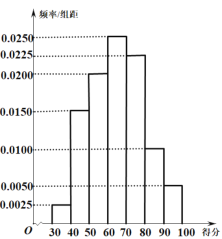
(1)请利用正态分布的知识求![]() ;
;
(2)该市食品安全检测部门为此次参加问卷调查的学生家长制定如下奖励方案:
①得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费:
的可以获赠1次随机话费:
②每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) |
|
|
概率 |
|
|
市食品安全检测部门预计参加此次活动的家长约5000人,请依据以上数据估计此次活动可能赠送出多少话费?
附:①![]() ;②若
;②若![]() ;则
;则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是![]() 年我国就业人口及劳动年龄人口(劳动年龄人口包含就业人口)统计表:
年我国就业人口及劳动年龄人口(劳动年龄人口包含就业人口)统计表:
时间(年) |
|
|
|
|
|
|
|
就业人口(万人) |
|
|
|
|
|
|
|
劳动年龄人口(万人) |
|
|
|
|
|
|
|
则由表可知( )
A.![]() 年我国就业人口逐年减少
年我国就业人口逐年减少
B.![]() 年我国劳动年龄人口逐年增加
年我国劳动年龄人口逐年增加
C.![]() 年这
年这![]() 年我国就业人口数量的中位数为
年我国就业人口数量的中位数为![]()
D.![]() 年我国劳动年龄人口中就业人口所占比重逐年增加
年我国劳动年龄人口中就业人口所占比重逐年增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为2的正方形.

(1)证明:A1C1![]() 平面ACD1;
平面ACD1;
(2)求异面直线CD与AD1所成角的大小;
(3)已知三棱锥D1﹣ACD的体积为![]() ,求AA1的长.
,求AA1的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 中有一题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马,”马主曰:“我马食半牛”,今欲衰偿之,问各出几何?其意:今有牛、马、羊吃了别人的禾苗,苗主人要求赔偿五斗粟,羊主人说:“我羊所吃的禾苗只有马的一半”马主人说:“我马所吃的禾苗只有牛的一半”打算按此比例偿还,问羊的主人应赔偿______斗粟,在这个问题中牛主人比羊主人多赔偿______斗粟.
中有一题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马,”马主曰:“我马食半牛”,今欲衰偿之,问各出几何?其意:今有牛、马、羊吃了别人的禾苗,苗主人要求赔偿五斗粟,羊主人说:“我羊所吃的禾苗只有马的一半”马主人说:“我马所吃的禾苗只有牛的一半”打算按此比例偿还,问羊的主人应赔偿______斗粟,在这个问题中牛主人比羊主人多赔偿______斗粟.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com