
【题目】某超市计划按月订购一种酸奶,每天进货量相同,已知每售出一箱酸奶的利润为50元,当天未售出的酸奶降价处理,以每箱亏损10元的价格全部处理完.若供不应求,可从其它商店调拨,每销售1箱可获利30元.假设该超市每天的进货量为14箱,超市的日利润为y元.为确定以后的订购计划,统计了最近50天销售该酸奶的市场日需求量,其频率分布表如图所示.
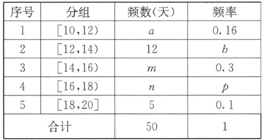
(1)求![]() 的值;
的值;
(2)求y关于日需求量![]() 的函数表达式;
的函数表达式;
(3)以50天记录的酸奶需求量的频率作为酸奶需求量发生的概率,估计日利润在区间[580,760]内的概率.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点
的中心在原点![]() ,焦点在
,焦点在![]() 轴上,左右焦点分别为
轴上,左右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,右焦点到右顶点的距离为1.
,右焦点到右顶点的距离为1.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,则
,则![]() 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任利用周末时间对该班级![]() 年最后一次月考的语文作文分数进行统计,发现分数都位于
年最后一次月考的语文作文分数进行统计,发现分数都位于![]() 之间,现将所有分数情况分为
之间,现将所有分数情况分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共七组,其频率分布直方图如图所示,已知
共七组,其频率分布直方图如图所示,已知![]() .
.

(1)求频率分布直方图中![]() 、
、![]() 的值;
的值;
(2)求该班级这次月考语文作文分数的平均数和中位数.(每组数据用该组区间中点值作为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解广大学生家长对校园食品安全的认识,某市食品安全检测部门对该市家长进行了一次校园食品安全网络知识问卷调查,每一位学生家长仅有一次参加机会,现对有效问卷进行整理,并随机抽取出了200份答卷,统计这些答卷的得分(满分:100分)制出的频率分布直方图如图所示,由频率分布直方图可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为这200人得分的平均值(同一组数据用该组区间的中点值作为代表).
近似为这200人得分的平均值(同一组数据用该组区间的中点值作为代表).
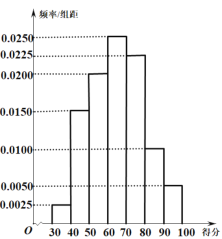
(1)请利用正态分布的知识求![]() ;
;
(2)该市食品安全检测部门为此次参加问卷调查的学生家长制定如下奖励方案:
①得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费:
的可以获赠1次随机话费:
②每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) |
|
|
概率 |
|
|
市食品安全检测部门预计参加此次活动的家长约5000人,请依据以上数据估计此次活动可能赠送出多少话费?
附:①![]() ;②若
;②若![]() ;则
;则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是![]() 年我国就业人口及劳动年龄人口(劳动年龄人口包含就业人口)统计表:
年我国就业人口及劳动年龄人口(劳动年龄人口包含就业人口)统计表:
时间(年) |
|
|
|
|
|
|
|
就业人口(万人) |
|
|
|
|
|
|
|
劳动年龄人口(万人) |
|
|
|
|
|
|
|
则由表可知( )
A.![]() 年我国就业人口逐年减少
年我国就业人口逐年减少
B.![]() 年我国劳动年龄人口逐年增加
年我国劳动年龄人口逐年增加
C.![]() 年这
年这![]() 年我国就业人口数量的中位数为
年我国就业人口数量的中位数为![]()
D.![]() 年我国劳动年龄人口中就业人口所占比重逐年增加
年我国劳动年龄人口中就业人口所占比重逐年增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间.
的单调区间.
(2)设直线![]() 是曲线
是曲线![]() 的切线,若
的切线,若![]() 的斜率存在最小值-2,求
的斜率存在最小值-2,求![]() 的值,并求取得最小斜率时切线
的值,并求取得最小斜率时切线![]() 的方程.
的方程.
(3)已知![]() 分别在
分别在![]() ,
,![]() 处取得极值,求证:
处取得极值,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为2的正方形.

(1)证明:A1C1![]() 平面ACD1;
平面ACD1;
(2)求异面直线CD与AD1所成角的大小;
(3)已知三棱锥D1﹣ACD的体积为![]() ,求AA1的长.
,求AA1的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() ax﹣lnx(a∈R).
ax﹣lnx(a∈R).
(1)若a=2时,求函数f(x)的单调区间;
(2)设g(x)=f(x)![]() 1,若函数g(x)在
1,若函数g(x)在![]() 上有两个零点,求实数a的取值范围.
上有两个零点,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com