
【题目】已知函数![]() ,且数列
,且数列![]() 满足
满足![]() .
.
(1)若数列![]() 是等差数列,求数列
是等差数列,求数列![]() 的通项公式;
的通项公式;
(2)若对任意的![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设等差数列![]() 的公差为
的公差为![]() ,由已知条件得出
,由已知条件得出![]() ,由
,由![]() 和
和![]() 可得出关于
可得出关于![]() 和
和![]() 的方程组,解出这两个量的值,利用等差数列的通项公式可求得
的方程组,解出这两个量的值,利用等差数列的通项公式可求得![]() ;
;
(2)推导出![]() ,可知数列
,可知数列![]() 中的奇数项和偶数项分别成以
中的奇数项和偶数项分别成以![]() 为公差的等差数列,以此求出数列
为公差的等差数列,以此求出数列![]() 的通项公式,然后分
的通项公式,然后分![]() 为奇数和偶数两种情况讨论,结合
为奇数和偶数两种情况讨论,结合![]() 恒成立,利用参变量分离法可求得
恒成立,利用参变量分离法可求得![]() 的取值范围.
的取值范围.
(1)设等差数列![]() 的公差为
的公差为![]() ,依题意得
,依题意得![]() ,故
,故![]() ,
,
则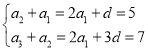 ,解得
,解得![]() ,
,![]()
因此,数列![]() 的通项公式为
的通项公式为![]() ;
;
(2)由(1)知,当![]() 时,
时,![]() ,①,
,①,![]() ,②
,②
两式相减得![]() ,
,
![]() 数列
数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列,数列
为公差的等差数列,数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列
为公差的等差数列
又![]()
![]() ,
,
当![]() 为偶数时,
为偶数时,![]() ;
;
当![]() 为奇数时,
为奇数时,![]() .
.
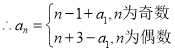 .
.
因为对任意的![]() 都有
都有![]() 成立,
成立,
当![]() 为奇数时,
为奇数时,![]() 恒成立,
恒成立,
![]() 在
在![]() 为奇数时恒成立,
为奇数时恒成立,![]() 即,
即,![]() ;
;
同理当![]() 为偶数时,
为偶数时,![]() 恒成立,
恒成立,
![]() 在
在![]() 为偶数时恒成立,
为偶数时恒成立,![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,已知每售出一箱酸奶的利润为50元,当天未售出的酸奶降价处理,以每箱亏损10元的价格全部处理完.若供不应求,可从其它商店调拨,每销售1箱可获利30元.假设该超市每天的进货量为14箱,超市的日利润为y元.为确定以后的订购计划,统计了最近50天销售该酸奶的市场日需求量,其频率分布表如图所示.
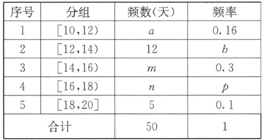
(1)求![]() 的值;
的值;
(2)求y关于日需求量![]() 的函数表达式;
的函数表达式;
(3)以50天记录的酸奶需求量的频率作为酸奶需求量发生的概率,估计日利润在区间[580,760]内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (其中
(其中![]() ,
,![]() 为自然对数的底数).
为自然对数的底数).
①![]() ,使得直线
,使得直线![]() 为函数
为函数![]() 的一条切线;
的一条切线;
②对![]() ,函数
,函数![]() 的导函数
的导函数![]() 无零点;
无零点;
③对![]() ,函数
,函数![]() 总存在零点;
总存在零点;
则上述结论正确的是______.(写出所有正确的结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
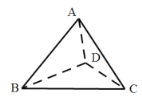
【题目】已知平面四边形![]() 中,
中,![]() ,
,![]() ,再将
,再将![]() 沿着
沿着![]() 翻折成三棱锥
翻折成三棱锥![]() 的过程中,直线
的过程中,直线![]() 与平面
与平面![]() 所成角均小于直线
所成角均小于直线![]() 与平面
与平面![]() 所成角,设二面角
所成角,设二面角![]() ,
,![]() 的大小分别为
的大小分别为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.存在
C.存在![]() D.存在
D.存在![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时期著名的数学家刘徽对推导特殊数列的求和公式很感兴趣,创造并发展了许多算法,展现了聪明才智.他在《九章算术》“盈不足”章的第19题的注文中给出了一个特殊数列的求和公式.这个题的大意是:一匹良马和一匹驽马由长安出发至齐地,长安与齐地相距3000里(1里=500米),良马第一天走193里,以后每天比前一天多走13里.驽马第一天走97里,以后每天比前一天少走半里.良马先到齐地后,马上返回长安迎驽马,问两匹马在第几天相遇( )
A. 14天B. 15天C. 16天D. 17天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大气污染是我国目前最突出的环境问题之一,其中工厂废气是大气污染的重大污染源之一。工厂废气未经净化处理排放至空气中,除了对空气质量造成严重破坏,还会对人体的健康造成重大威胁。长期生活在污染的空气中,生活质量及身体健康将急剧下降。某工厂因为污染问题需改进技术,2019年初购进一台环保新机器投入生产,机器的成本价为36万元,第![]() 年该机器包括维修费和机器护理费用在内,每年另需投人费用
年该机器包括维修费和机器护理费用在内,每年另需投人费用![]() 万元,购进该机器后每年盈利20万元.
万元,购进该机器后每年盈利20万元.
(1)问该机器投入生产第几年,工厂开始盈利(即总收入大于所有投人的费用)?
(2)由于机器使用年限越大维修等费用越高,所以工厂决定当年平均利润最大时将该机器以5万元低价处理,问使用该机器几年后工厂年平均利润最大?此时工厂获得的总利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 的长轴长为4.
的长轴长为4.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,是否存在实数
两点,是否存在实数![]() 使得以线段
使得以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com