
分析 先将原函数分离常数,然后结合指数函数的性质,再求含有自变量部分的式子的范围,则问题可解.
解答 解:由已知原函数可化为:$f(x)=\frac{{2}^{x}+1-2}{{2}^{x}+1}=1-\frac{2}{{2}^{x}+1}$.
因为2x>0,所以2x+1>1,
所以0$<\frac{2}{{2}^{x}+1}<2$,所以$-2<-\frac{2}{{2}^{x}+1}<0$,
所以$-1<1-\frac{2}{{2}^{x}+1}<1$,
所以要使对任意的x∈R,不等式f(x)<a恒成立,
只需a≥1即可.
故所求a的范围是[1,+∞).
点评 本题考查了指数函数的性质,不等式恒成立问题转化为函数最值问题的解题思路.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{5}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,$\overrightarrow{BP}$=$\overrightarrow{DA}$.
如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,$\overrightarrow{BP}$=$\overrightarrow{DA}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{π}{4}$) | B. | [$\frac{π}{4}$,$\frac{π}{2}$) | C. | ($\frac{π}{2}$,$\frac{3}{4}$π] | D. | [$\frac{3}{4}$π,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
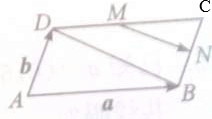 如图,?ABCD中,M、N分别是边DC、BC的中点.
如图,?ABCD中,M、N分别是边DC、BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com