已知抛物线C:y2=2px的焦点为F.P为C上异于原点的任意一点.过点P的直线l交C于另一点Q.交x轴的正半轴于点S.且有|FP|=|FS|．当点P的横坐标为3时.|PF|=|PS|．(Ⅰ)求C的方程,(Ⅱ)若直线l1∥l.且l1和C有且只有一个公共点E．(ⅰ)证明直线PE过定点.并求出定点坐标,(ⅱ)△PQE的面积是否存在最小值?若存在.请求出最小值,若不存在.请说明� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

10．已知抛物线C：y²=2px（p＞0）的焦点为F，P为C上异于原点的任意一点，过点P的直线l交C于另一点Q，交x轴的正半轴于点S，且有|FP|=|FS|．当点P的横坐标为3时，|PF|=|PS|．
（Ⅰ）求C的方程；
（Ⅱ）若直线l₁∥l，且l₁和C有且只有一个公共点E．
（ⅰ）证明直线PE过定点，并求出定点坐标；
（ⅱ）△PQE的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．

分析（Ⅰ）根据抛物线的焦半径公式，结合等边三角形的性质，求出的p值；
（Ⅱ）（ⅰ）设出点P的坐标，求出直线PQ的方程，利用直线l₁∥l，且l₁和C有且只有一个公共点E，求出点E的坐标，写出直线PE的方程，将方程化为点斜式，可求出定点；
（ⅱ）利用弦长公式求出弦PQ的长度，再求点E到直线PQ的距离，得到关于面积的函数关系式，再利用基本不等式求最小值．

解答解：（I）如图所示，由题意可得：x_P=3时，△PFS是等边三角形，|PF|=3+$\frac{p}{2}$，
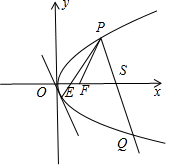
∴3-$\frac{p}{2}$=$\frac{1}{2}$$（3+\frac{p}{2}）$，解得p=2．∴抛物线C的方程为：y²=4x．
（II）（i）证明：设P（x₁，y₁），${y}_{1}^{2}=4{x}_{1}$，
∵|FP|=|FS|=x₁+1，
∴S（x₁+2，0），
∴k_PQ=-$\frac{{y}_{1}}{2}$．
由直线l₁∥l可设直线l₁方程为y=-$\frac{{y}_{1}}{2}$x+m，
联立方程$\left\{\begin{array}{l}{y=-\frac{{y}_{1}}{2}x+m}\\{{y}^{2}=4x}\end{array}\right.$，消去x得${y}_{1}{y}^{2}$+8y-8m=0 ①
由l₁和C有且只有一个公共点得△=64+32y₁m=0，∴y₁m=-2，
这时方程①的解为y=-$\frac{4}{{y}_{1}}$，代入y=-$\frac{{y}_{1}}{2}$x+m，
得x=m²，∴E（m²，2m）．
点P的坐标可化为$（\frac{1}{{m}^{2}}，-\frac{2}{m}）$，直线PE方程为y-2m=$\frac{-\frac{2}{m}-2m}{\frac{1}{{m}^{2}}-{m}^{2}}$（x-m²），
即y-2m=$\frac{2m}{{m}^{2}-1}$（x-m²），
令y=0，可得x=1，
∴直线AE过定点（1，0）．
（ⅱ）设Q（x₂，y₂）．
直线PQ的方程为$y-{y}_{1}=-\frac{{y}_{1}}{2}$$（x-\frac{{y}_{1}^{2}}{4}）$，即x=-$\frac{2}{{y}_{1}}y$+$\frac{{y}_{1}^{2}}{4}$+2．
联立方程$\left\{\begin{array}{l}{x=-\frac{2}{{y}_{1}}y+\frac{{y}_{1}^{2}}{4}+2}\\{{y}^{2}=4x}\end{array}\right.$，消去x得y²+$\frac{8}{{y}_{1}}$y-$（{y}_{1}^{2}+8）$=0，
∴y₁+y₂=-$\frac{8}{{y}_{1}}$，y₁y₂=-$（{y}_{1}^{2}+8）$，
∴|PQ|=$\sqrt{1+\frac{4}{{y}_{1}^{2}}}$|y₁-y₂|=$\sqrt{1+\frac{4}{{y}_{1}^{2}}}$$\sqrt{（{y}_{1}+{y}_{2}）^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{1+\frac{4}{{y}_{1}^{2}}}$$|2{y}_{1}+\frac{8}{{y}_{1}}|$．
∴E$（\frac{4}{{y}_{1}^{2}}，-\frac{4}{{y}_{1}}）$，
点E到直线PQ的距离为：d=$\frac{|\frac{4}{{y}_{1}^{2}}-\frac{8}{{y}_{1}^{2}}-\frac{{y}_{1}^{2}}{4}-2|}{\sqrt{1+\frac{4}{{y}_{1}^{2}}}}$=$\frac{|\frac{4}{{y}_{1}^{2}}+\frac{{y}_{1}^{2}}{4}+2|}{\sqrt{1+\frac{4}{{y}_{1}^{2}}}}$，
∴△ABE的面积S=$\frac{1}{2}$d|PQ|=$|{y}_{1}+\frac{4}{{y}_{1}}|•$$|\frac{4}{{y}_{1}^{2}}+\frac{{y}_{1}^{2}}{4}+2|$≥$2\sqrt{{y}_{1}•\frac{4}{{y}_{1}}}$$•（2\sqrt{\frac{2}{{y}_{1}}•\frac{{y}_{1}}{2}}）^{2}$=16，
当且仅当y₁=±2时等号成立，
∴△ABE的面积最小值为16．

点评本题考查了抛物线的定义标准方程及其性质、直线与抛物线相交弦长问题、直线与抛物线相切切线问题、点到直线的距离公式、三角形面积计算公式、基本不等式的性质，考查了推理能力与计算能力，属于难题．

练习册系列答案

开心语文现代文阅读技能训练100篇系列答案

现代文阅读新选精练系列答案

文言文译注及赏析系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

20．（1）已知sin⁴θ+cos⁴θ=$\frac{5}{9}$，求sin2θ的值；
（2）化简：sin40°（tan10°-$\sqrt{3}$）

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

1．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的离心率为2，过右焦点F作直线交该双曲线于A、B两点，P为x轴上一点，且|PA|=|PB|，若|AB|=8，则|FP|=（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

18．按照国家规定，某种大米质量（单位：kg）必须服从正态分布ξ～N（10，σ²），根据检测结果可知P（9.9≤ξ≤10.1）=0.96，某公司为每位职工购买一袋这种包装的大米作为福利，若该公司有2000名职工，则分发到的大米质量在9.9kg以下的职工数大约为40．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

5．已知随机变量ξ～B（5，$\frac{1}{3}$），则P（ξ=3）=（　　）

A．

$\frac{5}{27}$

B．

$\frac{7}{81}$

C．

$\frac{40}{243}$

D．

$\frac{19}{144}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

15．某中学采用系统抽样方法，从该校高一年级全体800名学生中抽80名学生做牙齿健康检查．现将800名学生从1到800进行编号．已知从31～40这10个数中取的数是39，则在第1小组1～10中随机抽到的数是9．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

2．下列说法不正确的是（　　）

	A．	“若xy=0，则x=0或y=0”的否命题是真命题
	B．	命题“?x∈R，x²-x-1＜0”的否定是“?x∈R，x²-x-1≥0”
	C．	?x∈R，使得e^x＜x-1
	D．	“a＜0”是“x²+ay²=1表示双曲线”的充要条件．