
| A. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,则$\overrightarrow{a}$=$\overrightarrow{b}$ | B. | 若$\overrightarrow{a}$,$\overrightarrow{b}$都是单位向量,则$\overrightarrow{a}$=$\overrightarrow{b}$ | ||
| C. | 若$\overrightarrow{a}$=$\overrightarrow{0}$,$\overrightarrow{b}$=0,则$\overrightarrow{a}$=$\overrightarrow{b}$ | D. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|且$\overrightarrow{a}∥\overrightarrow{b}$,则$\overrightarrow{a}$=$\overrightarrow{b}$ |
分析 根据平面向量相等是模长相等,方向相同,对选项中的命题进行判断即可.
解答 解:对于A,当|$\overrightarrow{a}$|=|$\overrightarrow{b}$|时,$\overrightarrow{a}$=$\overrightarrow{b}$不一定成立,∴命题A错误;
对于B,当$\overrightarrow{a}$,$\overrightarrow{b}$都是单位向量时,$\overrightarrow{a}$=$\overrightarrow{b}$不一定成立,∴命题B错误;
对于C,当$\overrightarrow{a}$=$\overrightarrow{0}$,$\overrightarrow{b}$=$\overrightarrow{0}$时,则$\overrightarrow{a}$=$\overrightarrow{b}$=$\overrightarrow{0}$,命题C正确;
对于D,当|$\overrightarrow{a}$|=|$\overrightarrow{b}$|且$\overrightarrow{a}∥\overrightarrow{b}$时,$\overrightarrow{a}$=$\overrightarrow{b}$或$\overrightarrow{a}$=-$\overrightarrow{b}$,∴命题D错误.
故选:C.
点评 本题考查了平面向量相等的应用问题,是基础题目.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
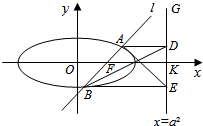 如图,已知直线l:x=my+1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
如图,已知直线l:x=my+1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{n}^{9}$x9 | B. | C${\;}_{n}^{8}$x8 | C. | C${\;}_{n}^{9}$xn-9 | D. | C${\;}_{n}^{8}$xn-8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 我国对PM2.5采用如下标准:
我国对PM2.5采用如下标准:| PM2.5日均值m(微克/立方米) | 空气质量等级 |
| m<35 | 一级 |
| 35≤m≤75 | 二级 |
| m>75 | 超标 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.35 | B. | 0.30 | C. | 0.25 | D. | 0.20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,π] | B. | [0,$\sqrt{2}$π] | C. | [0,$\sqrt{3}π$] | D. | [0,2π] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com