
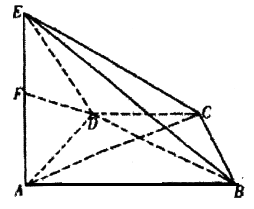
【题目】如图,底面为等腰梯形的四棱锥 ![]() 中,
中, ![]() 平面
平面 ![]() ,
, ![]() 为
为 ![]() 的中点,
的中点, ![]() ,
, ![]() ,
, ![]() .
.
(1)证明: ![]() 平面
平面 ![]() ;
;
(2)若 ![]() ,求三棱锥
,求三棱锥 ![]() 的体积.
的体积.
【答案】
(1)证明:取 ![]() 的中点
的中点 ![]() ,连接
,连接 ![]() ,
, ![]() ,因为
,因为 ![]() 为
为 ![]() 的中点,
的中点,
所以 ![]()
![]() ,
,
又因为 ![]() ,
, ![]()
![]() ,
,
所以四边形 ![]() 是平行四边形,
是平行四边形,
所以 ![]() ,又
,又 ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
,
所以 ![]() 平面
平面 ![]() .
.
(2)解:等腰梯形 ![]() 中,作
中,作 ![]() 于
于 ![]() ,则
,则 ![]() ,在
,在 ![]() 中,
中, ![]() ,则
,则![]() ,即点
,即点 ![]() 到
到 ![]() 的距离
的距离 ![]() ,又
,又 ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,所以
,所以 ![]() ,又
,又 ![]() ,∴
,∴ ![]() 平面
平面 ![]() .
.
∴三棱锥 ![]() 的体积
的体积 ![]()
![]() .
.
【解析】(1)取 E B 的中点 G ,连接 F G , C G ,由中位线性质不难得到DFGC为平行四边形,故D F / / C G ,又 D F 平面 E B C , C G 平面 E B C ,所以 ![]() 平面
平面 ![]() .(2)等腰梯形ABCD中,作CH⊥AB于H,求出点B到CD的距离,即可求出三棱锥B-CDE的体积.
.(2)等腰梯形ABCD中,作CH⊥AB于H,求出点B到CD的距离,即可求出三棱锥B-CDE的体积.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某分公司经销某种品牌产品,每件产品的成本为30元,并且每件产品须向总公司缴纳a元(a为常数,2≤a≤5)的管理费,根据多年的统计经验,预计当每件产品的售价为x元时,产品一年的销售量为 ![]() (e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(1)求分公司经营该产品一年的利润L(x)万元与每件产品的售价x元的函数关系式;
(2)当每件产品的售价为多少元时,该产品一年的利润L(x)最大,并求出L(x)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断错误的是( )
A.若随机变量 ![]() 服从正态分布
服从正态分布 ![]() ,则
,则 ![]() ;
;
B.若 ![]() 组数据
组数据 ![]() 的散点都在
的散点都在 ![]() 上,则相关系数
上,则相关系数 ![]() ;
;
C.若随机变量 ![]() 服从二项分布:
服从二项分布: ![]() , 则
, 则 ![]() ;
;
D.![]() 是
是 ![]() 的充分不必要条件;
的充分不必要条件;
查看答案和解析>>
科目:高中数学 来源: 题型:
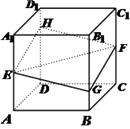
【题目】如图,正方体 ![]() 的棱长为1,
的棱长为1, ![]() 分别是棱
分别是棱 ![]() 的中点,过
的中点,过 ![]() 的平面与棱
的平面与棱 ![]() 分别交于点
分别交于点 ![]() .设
.设 ![]() ,
, ![]() .
.
①四边形 ![]() 一定是菱形;②
一定是菱形;② ![]() 平面
平面 ![]() ;③四边形
;③四边形 ![]() 的面积
的面积 ![]() 在区间
在区间 ![]() 上具有单调性;④四棱锥
上具有单调性;④四棱锥 ![]() 的体积为定值.
的体积为定值.
以上结论正确的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,该几何体是由一个直三棱柱 ![]() 和一个正四棱锥
和一个正四棱锥 ![]() 组合而成,
组合而成, ![]() ,
, ![]() .
.
(Ⅰ)证明:平面 ![]() 平面
平面 ![]() ;
;
(Ⅱ)求正四棱锥 ![]() 的高
的高 ![]() ,使得二面角
,使得二面角 ![]() 的余弦值是
的余弦值是 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(I)若曲线 ![]() 存在斜率为-1的切线,求实数a的取值范围;
存在斜率为-1的切线,求实数a的取值范围;
(II)求 ![]() 的单调区间;
的单调区间;
(III)设函数 ![]() ,求证:当
,求证:当 ![]() 时,
时, ![]() 在
在 ![]() 上存在极小值.
上存在极小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com