
已知a>1,f(logax)=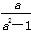 ·(x-
·(x- ).
).
(1)求f(x);
(2)判断并证明f(x)的单调性;
(3)若f(1-m)+f(2m)<0,求m的取值范围.
[解析] (1)设t=logax,则x=at,
则f(t)=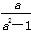 (at-
(at-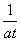 ),
),
∴f(x)=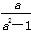 (ax-a-x)(x∈R).
(ax-a-x)(x∈R).
(2)设x1<x2,则f(x1)-f(x2)=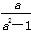 (ax1-a-x1)-
(ax1-a-x1)-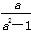 (ax2-a-x2)
(ax2-a-x2)
=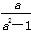 [(ax1-ax2)+(a-x2-a-x1)]
[(ax1-ax2)+(a-x2-a-x1)]
=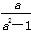 (ax1-ax2)(1+
(ax1-ax2)(1+ ).
).
∵a>1,∴ax1<ax2,则有ax1-ax2<0.
而 >0,1+
>0,1+ >0,
>0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
∴函数f(x)为R上的增函数.
(3)∵f(-x)= (a-x-ax)
(a-x-ax)
=- (ax-a-x)=-f(x),
(ax-a-x)=-f(x),
∴f(x)为奇函数.
∵f(1-m)+f(2m)<0,
∴f(1-m)<-f(2m)=f(-2m).
∵f(x)在R上是增函数,
∴1-m<-2m.
解得m<-1.
故m的取值范围是(-∞,-1).


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
夏季高山温度从山脚起每升高100米,降低0.7摄氏度,已知山顶的温度是14.1摄氏度,山脚的温度是26摄氏度,则山的相对高度为( )
A.1750米 B.1730米
C.1700米 D.1680米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com