
分析 (1)根据产品的利润=销售额-产品的成本,建立函数关系;
(2)利用基本不等式可求出该函数的最值,注意等号成立的条件,对能否取得等号进行分类讨论,即可得出答案.
解答 解:(1)由题意知,y=(4+$\frac{20}{P}$)P-x-(10+2P),
将$P=3-\frac{2}{x+1}$(其中0≤x≤a,a为正常数)代入化简得y=16-$\frac{4}{x+1}$-x(0≤x≤a),
故该产品的利润y万元表示为促销费用x万元的函数为y=16-$\frac{4}{x+1}$-x(0≤x≤a),
(2)y=17-($\frac{4}{x+1}$+x+1)≤17-2$\sqrt{\frac{4}{x+1}×(x+1)}$=13,
当且仅当$\frac{4}{x+1}$=x+1,即x=1时,上式取等号,
①当a≥1时,促销费用投入1万元时,厂家的利润最大;
②当a<1时,y=17-($\frac{4}{x+1}$+x+1)在[0,a]上单调递增,
∴x=a时,函数有最大值.即促销费用投入a万元时,厂家的利润最大.
综上,当a≥1时,促销费用投入1万元,厂家的利润最大;
当a<1时,促销费用投入a万元,厂家的利润最大.
点评 本题考查基本不等式在最值问题中的应用,考查分类讨论的数学思想,属于中档题.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-$\frac{1}{2}$,$\frac{3}{2}$) | C. | (-$\frac{1}{5}$,$\frac{3}{5}$) | D. | (-$\frac{1}{7}$,$\frac{3}{7}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-2)2+(y+1)2=4 | B. | (x+2)2+(y-1)2=4 | C. | (x-2)2+(y+1)2=16 | D. | (x+2)2+(y-1)2=16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
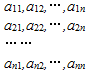 设A1,A2,…,An(n≥4)为集合S={1,2,…,n}的n个不同子集,为了表示这些子集,作n行n列的数阵,规定第i行第j列的数为:${a_{ij}}=\left\{\begin{array}{l}0,\;i∉{A_j}\\ 1,\;i∈{A_j}\end{array}\right.$.则下列说法中,错误的是( )
设A1,A2,…,An(n≥4)为集合S={1,2,…,n}的n个不同子集,为了表示这些子集,作n行n列的数阵,规定第i行第j列的数为:${a_{ij}}=\left\{\begin{array}{l}0,\;i∉{A_j}\\ 1,\;i∈{A_j}\end{array}\right.$.则下列说法中,错误的是( )| A. | 数阵中第一列的数全是0当且仅当A1=∅ | |
| B. | 数阵中第n列的数全是1当且仅当An=S | |
| C. | 数阵中第j行的数字和表明集合Aj含有几个元素 | |
| D. | 数阵中所有的n2个数字之和不超过n2-n+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com