练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．i为虚数单位，若（$\sqrt{3}$+i）z=$\sqrt{3}$-1，那么|z|=（　　）
    A．1B．$\sqrt{\frac{2-\sqrt{3}}{2}}$C．$\sqrt{\frac{4+\sqrt{3}}{2}}$D．2

    分析 把已知等式变形，利用复数代数形式的乘除运算化简，再代入复数模的计算公式得答案．

    解答 解：∵（$\sqrt{3}$+i）z=$\sqrt{3}$-1，
    ∴$z=\frac{\sqrt{3}-1}{\sqrt{3}+i}=\frac{（\sqrt{3}-1）（\sqrt{3}-i）}{（\sqrt{3}+i）（\sqrt{3}-i）}$=$\frac{3-\sqrt{3}}{4}-\frac{\sqrt{3}-1}{4}i$．
    ∴|z|=$\sqrt{（\frac{3-\sqrt{3}}{4}）^{2}+（-\frac{\sqrt{3}-1}{4}）^{2}}=\sqrt{\frac{2-\sqrt{3}}{2}}$．
    故选：B．

    点评 本题考查复数代数形式的乘除运算，考查了复数模的求法，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届山东潍坊临朐县高三10月月考数学（理）试卷（解析版） 题型：解答题

    已知命题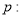指数函数在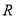上是单调函数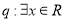；命题，.若命题“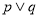”为真命题，命题“”为假命题，求实数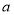的取值范围.

    查看答案和解析>>

    科目：高中数学 来源：2017届湖南长沙长郡中学高三上周测十二数学（文）试卷（解析版） 题型：解答题

    某志愿者到某山区小学支教，为了解留守儿童的幸福感，该志愿者对某班40名学生进行了一次幸福指数的调查问卷，并用茎叶图表示如图（注：图中幸福指数低于70，说明孩子幸福感弱；幸福指数不低于70，说明孩子幸福感强）．

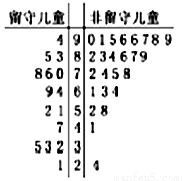
    （1）根据茎叶图中的数据完成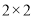列联表，并判断能否有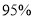的把握认为孩子的幸福感强与是否是留守儿童有关？

    幸福感强

    幸福感弱

    总计

    留守儿童

    非留守儿童

    总计

    （2）从15个留守儿童中按幸福感强弱进行分层抽样，共抽取5人，又在这5人中随机抽取2人进行家访，求这2个学生中恰有一人幸福感强的概率．

    参考公式：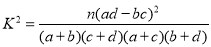

    附表：

    0.050

    0.010

    3.841

    6.635

    查看答案和解析>>

    科目：高中数学 来源：2017届湖南长沙长郡中学高三上周测十二数学（文）试卷（解析版） 题型：选择题

    若复数满足（为虚数单位），则复数的虚部为（ ）

    A．1 B．

    C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）图象相邻的一个最大值点和一个对称中心分别为（$\frac{π}{6}$，2），（$\frac{5π}{12}$，0），则g（x）=f（x）cos2x在区间[0，$\frac{π}{4}$）的值域为[0，$\frac{3}{2}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．设点P（x，y）是不等式组$\left\{\begin{array}{l}{y≥0}\\{x-2y+1≥0}\\{x+y≤3}\end{array}\right.$，所表示的平面区域内的任意一点，向量$\overrightarrow{m}$=（1，1），$\overrightarrow{n}$=（2，1），点O是坐标原点．若向量$\overrightarrow{OP}$=λ$\overrightarrow{m}$+μ$\overrightarrow{n}$（λ，μ∈R），则λ-μ的取值范围是（　　）
    A．[-$\frac{3}{2}$，$\frac{2}{3}$]B．[-6，2]C．[-1，$\frac{7}{2}$]D．[-4，$\frac{2}{3}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．定义区间[x1，x2]的长度为x2-x1（x2＞x1）单调递增），函数$f（x）=\frac{{（{a^2}+a）x-1}}{{{a^2}x}}$（a∈R，a≠0）的定义域与值域都是[m，n]（n＞m），则区间[m，n]取最大长度时实数a的值（　　）
    A．$\frac{{2\sqrt{3}}}{3}$B．-3C．1D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．设α，β是两个平面，直线a?α则“a∥β”是“α∥β”的（　　）
    A．充分而不必要条件B．必要而不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．某公司要招聘甲、乙两类员工共150人，该公司员工的工资由基础工资组成．其中甲、乙两类员工每人每月的基础工资分别为2千元和3千元，甲类员工每月的人均绩效工资与公司月利润成正比，比例系数为a（a＞0），乙类员工每月的绩效工资与公司月利润的平方成正比，比例系数为b（b＞0）．
    （Ⅰ）若要求甲类员工的人数不超过乙类员工人数的2倍，问甲、乙两类员工各招聘多少人时，公司每月所付基础工资总额最少？
    （Ⅱ）若该公司每月的利润为x（x＞0）千元，记甲、乙两类员工该月人均工资分别为w甲千元和w乙千元，试比较w甲和w乙的大小．（月工资=月基础工资+月绩效工资）

    查看答案和解析>>

    同步练习册答案