Question

13．根据我国发布的《环境空气质量指数AQI技术规定》（试行），AQI共分为六级：[0，50）为优，[50，100）为良，[100，150）为轻度污染，[150，200）为重度污染，[200，250），[250，300）均为重度污染，300及以上为严重污染．某市2015年11月份30天的AQI的频率分布直方图如图所示．
（1）该市11月份环境空气质量优或良共有多少天？
（2）若采用分层抽样方法从30天中抽取10天进行市民户外晨练人数调查，则重度污染被抽到的天数共有多少天？
（3）空气质量指数低于150时市民适宜户外晨练，该市民王先生决定某天早晨进行户外晨练，则他当天适宜户外晨练的概率是多少？

Answer 1

分析 （1）由频率分布直方图能求出该市11月环境空气质量优或良的天数．
（2）由频率分布直方图能求出重度污染被抽到的天数．
（3）设“市民王先生当天适宜户外晨练”为事件A，由频率分布直方图能求出他当天适宜户外晨练的概率．

解答 解：（1）由题意得该市11月环境空气质量优或良共有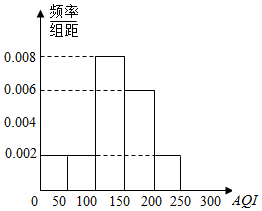

（0.002+0.002）×50×30=6（天）．
（2）重度污染被抽到的天数共有0.06×50×10=3（天）．
（3）设“市民王先生当天适宜户外晨练”为事件A，
则P（A）=（0.002+0.002+0.008）×50=0.6．

点评 本题考查频率分直方图的应用，考查概率的求法，是基础题，解题时要认真审题，注意频率分布直方图的合理运用．