
| x+2 |
| x+2 |
| x+2 |
|
| x+2 |
| x+2 |
|
| x+2 |
|
| 9 |
| 4 |
| 9 |
| 4 |


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
 如图在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x | 80 | 90 | 100 | 110 | 120 |
| y | 48 | 52 | 63 | 72 | 80 |
| |||||||
|
| |||||||
|
| Sxy | ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| a+x |
| b+x |
| a |
| b |
| a |
| b |
| sinA |
| sinB+sinC |
| sinB |
| sinC+sinA |
| sinC |
| sinA+sinB |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
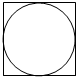 在图的正方形中随机撒一把芝麻,用随机模拟的方法估计圆周率π的值.如果撒了1000个芝麻,落在圆内的芝麻总数是781颗,那么这次模拟中π的估计值是
在图的正方形中随机撒一把芝麻,用随机模拟的方法估计圆周率π的值.如果撒了1000个芝麻,落在圆内的芝麻总数是781颗,那么这次模拟中π的估计值是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com