
 如图,在矩形ABCD中,BC=2,E,F分别为AB,CD的中点,且沿AF,BF分别将△AFD与△BFC折起来,使其顶点C与D重合于点P,若所得三棱锥P-ABF的顶点P在底面ABF内的射影O恰为EF的中点.
如图,在矩形ABCD中,BC=2,E,F分别为AB,CD的中点,且沿AF,BF分别将△AFD与△BFC折起来,使其顶点C与D重合于点P,若所得三棱锥P-ABF的顶点P在底面ABF内的射影O恰为EF的中点.分析 ( I )证明PF⊥面PAB,求出棱锥的底面面积与高,即可利用${V}_{P-ABF}^{\;}=\frac{1}{3}{S}_{△ABF}^{\;}•PO$求解体积.
(II)法一:先求二面角P-BF-O.作OH⊥BF于H,连PH,说明∠PHO为二面角P-BF-O的平面角,解Rt△PHO中,即可求解二面角C-BF-P的大小.
法二:设平面PBF与平面BCF的夹角为φ,求解法向量,求解平面BCF的一个法向量,利用数量积求解二面角为钝二面角.
解答 解:(I)依题设:$\left\{\begin{array}{l}PF⊥PA\\ PF⊥PB\\ PA∩PB=P\end{array}\right.$⇒PF⊥面PAB
又依题设:O为EF的中点,且PO⊥EF⇒PE=PF,故△PEF是斜边为EF=2的等腰Rt△,
故$PO=1,PE=PF=\sqrt{2}$,且$AB=DC=2PF=2\sqrt{2}$,
又ABCD为矩形,且E,F为边的中点EF⊥AB,
故$V_{P-ABF}^{\;}=\frac{1}{3}S_{△ABF}^{\;}•PO=\frac{1}{3}×2\sqrt{2}×1=\frac{{2\sqrt{2}}}{3}$.
(II) 法一:因所求二面角与二面角P-BF-O互补,故先求二面角P-BF-O.作OH⊥BF于H,连PH,
则由PO⊥面ABCD知:OH为PH的射影⇒PH⊥BF⇒∠PHO为二面角P-BF-O的平面角,
在Rt△PBE中,由PH•BF=PF•PB易求得:$PH=\frac{2}{{\sqrt{3}}}$,又PO=1,
故在Rt△PHO中,由$sin∠PHO=\frac{PO}{PH}=\frac{{\sqrt{3}}}{2}$⇒∠PHO=$\frac{π}{3}$,
由此即知二面角C-BF-P的大小为$\frac{2π}{3}$.
法二:设平面PBF与平面BCF的夹角为φ,并设
其法向量为$\overrightarrow{n}$=(x,y,z),则由$\overrightarrow{BF}$=$(-2,-\sqrt{2},0)$,
$\overrightarrow{PF}$=(-1,0,-1),以及$\left\{\begin{array}{l}\overrightarrow{n}•\overrightarrow{BF}=0\\ \overrightarrow{n}•\overrightarrow{PF}=0\end{array}\right.$,可得$\left\{\begin{array}{l}-2x-\sqrt{2}y=0\\-x-z=0\end{array}\right.$,即$\left\{\begin{array}{l}y=-\sqrt{2}x\\ z=-x\end{array}\right.$
取x=1,得平面PBF
的一个法向量为:$\overrightarrow{n}=(1,-\sqrt{2},-1)$;而平面BCF的一个法向量为:$\overrightarrow{m}=(0,0,1)$,
故由$cosϕ=|cos<\overrightarrow{n},\overrightarrow{m}>|$=$\frac{1}{2}$$⇒φ=\frac{π}{3}$.而所求二面角为钝二面角,
故其大小为$π-φ=\frac{2π}{3}$.
点评 本题考查空间几何体的体积以及二面角的求法,考查空间想象能力、逻辑推理能力以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=60°,AB=2AD,PD⊥平面ABCD,点M为PC上的点,且PM=2MC.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=60°,AB=2AD,PD⊥平面ABCD,点M为PC上的点,且PM=2MC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,在Rt△ABC中,∠ABC=90°,∠BAC=60°,AB=2,D,E分别为AC,BD的中点,连接AE并延长BC于F,将△ABD沿BD折起,使平面ABD⊥平面BCD,如图2,所示,
如图1,在Rt△ABC中,∠ABC=90°,∠BAC=60°,AB=2,D,E分别为AC,BD的中点,连接AE并延长BC于F,将△ABD沿BD折起,使平面ABD⊥平面BCD,如图2,所示,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的一块木料中,棱BC平行于面A′C′.
如图所示的一块木料中,棱BC平行于面A′C′.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四棱锥P-ABCD,AD∥BC,AB⊥BC,AD=2,AB=BC=PC=PD=1,∠APD=90°.
已知四棱锥P-ABCD,AD∥BC,AB⊥BC,AD=2,AB=BC=PC=PD=1,∠APD=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
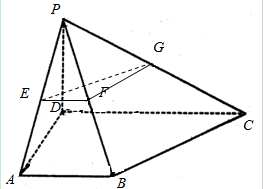 如图,在四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}$AD=1.
如图,在四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}$AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com