
已知函数
(1)若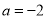 ,求证:函数
,求证:函数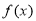 在(1,+∞)上是增函数;
在(1,+∞)上是增函数;
(2)当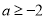 时,求函数
时,求函数 在[1,e]上的最小值及相应的x值;
在[1,e]上的最小值及相应的x值;
(3)若存在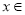 [l,e],使得
[l,e],使得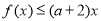 成立,求实数
成立,求实数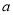 的取值范围.
的取值范围.
(1)详见解析;(2) 的最小值为1,相应的x值为1;(3)
的最小值为1,相应的x值为1;(3)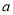 的取值范围是
的取值范围是 .
.
【解析】
试题分析:(1)当 时,
时, ,当
,当 ,
, ,因此要证
,因此要证 在
在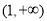 上是增函数,只需证明在
上是增函数,只需证明在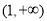 上有
上有 ,而这是显然成立的,故得证;(2)由(1)中的相关结论,可证当
,而这是显然成立的,故得证;(2)由(1)中的相关结论,可证当 时,
时, 在
在 上是增函数,
上是增函数, 在
在 上的最小值即为
上的最小值即为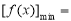
 ;(3)可将不等式
;(3)可将不等式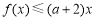 变形为
变形为 ,因此问题就等价于当
,因此问题就等价于当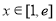 时,
时, 需满足
需满足 ,利用导数求函数
,利用导数求函数 在
在 上的单调性,可知
上的单调性,可知 在
在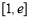 上为增函数,故
上为增函数,故 ,即
,即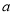 的取值范围是
的取值范围是 .
.
(1)当 时,
时, ,当
,当 ,
, ,
,
故函数 在
在 上是增函数 2分;
上是增函数 2分;
(2) ,当
,当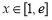 ,
, ,
,
当 时,
时,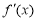 在
在 上非负(仅当
上非负(仅当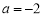 ,
,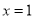 时,
时, ),
),
故函数 在
在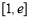 上是增函数,此时
上是增函数,此时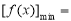
 .
.
∴当 时,
时, 的最小值为1,相应的
的最小值为1,相应的 值为1. 5分;
值为1. 5分;
(3)不等式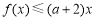 ,可化为
,可化为 .
.
∵ , ∴
, ∴ 且等号不能同时取,所以
且等号不能同时取,所以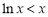 ,即
,即 ,
,
因而 (
( ),
),
令 (
( ),又
),又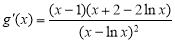 ,
,
当 时,
时, ,
,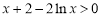 ,
,
从而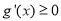 (仅当x=1时取等号),所以
(仅当x=1时取等号),所以 在
在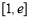 上为增函数,
上为增函数,
故 的最小值为
的最小值为 ,所以
,所以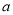 的取值范围是
的取值范围是 . 10分.
. 10分.
考点:1.利用导数判断函数单调性求极值;2.存在性问题的处理方法


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源:2015届天津市红桥区高二下学期期末考试理科数学试卷(解析版) 题型:填空题
在5道题中有3道历史类,两道诗词鉴赏类,如果不放回地依次抽取2道题,则在第一次抽到历史题的条件下,第二次抽到历史类问题的概率为 _________ .
查看答案和解析>>
科目:高中数学 来源:2015届天津市红桥区高二下学期期末考试文科数学试卷(解析版) 题型:填空题
把命题“若 是正实数,则有
是正实数,则有 ”推广到一般情形,推广后的命题为____________.
”推广到一般情形,推广后的命题为____________.
查看答案和解析>>
科目:高中数学 来源:2015届天津市红桥区高二下学期期末考试文科数学试卷(解析版) 题型:选择题
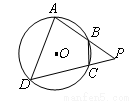
如图,四边形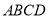 是圆
是圆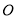 的内接四边形,延长
的内接四边形,延长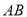 和
和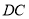 相交于点
相交于点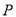 ,若
,若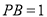 ,
,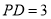 ,则
,则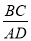 的值为( )
的值为( )
A.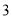 B.
B.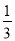 C.
C.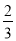 D.
D.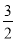
查看答案和解析>>
科目:高中数学 来源:2015届天津市红桥区高二下学期期中考试理科数学试卷(解析版) 题型:选择题
若函数 在(0,1)内有极小值,则实数b的取值范围是( )
在(0,1)内有极小值,则实数b的取值范围是( )
A.(0,1) B.(0, ) C.(0,+∞) D.(
) C.(0,+∞) D.( ∞,1)
∞,1)
查看答案和解析>>
科目:高中数学 来源:2015届天津市红桥区高二下学期期中考试文科数学试卷(解析版) 题型:填空题
下表是关于新生婴儿的性别与出生时间段调查的列联表,那么,A= ,B= ,C= ,D= .
| 晚上 | 白天 | 总计 |
男 | 45 | A | 92 |
女 | B | 35 | C |
总计 | 98 | D | 180 |
查看答案和解析>>
科目:高中数学 来源:2015届四川省资阳市高二下学期期末考试文科数学试卷(解析版) 题型:选择题
定义在R上的函数 ,若对任意
,若对任意 ,都
,都
有 ,则称f(x)为“H函数”,给出下列函数:①
,则称f(x)为“H函数”,给出下列函数:① ;②
;② ;③
;③ ;④
;④ 其中是“H函数”的个数为( ).
其中是“H函数”的个数为( ).
A.4 B.3 C.2 D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com