
| A. | [$\frac{5}{3}$,+∞) | B. | [$\frac{5}{4}$,+∞) | C. | (1,$\frac{5}{3}$] | D. | (1,$\frac{5}{4}$] |
分析 将x=c代入$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1和y=±$\frac{b}{a}$x,求出A,B,C,D的坐标,由两点之间的距离公式求得|AB|,|CD|,由|AB|≥$\frac{3}{5}$|CD|,求得a和c的关系,根据离心率公式,即可求得离心率的取值范围.
解答 解:当x=c时代入$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1得y=±$\frac{{b}^{2}}{a}$,则A(c,$\frac{{b}^{2}}{a}$),B(c,-$\frac{{b}^{2}}{a}$),则AB=$\frac{2{b}^{2}}{a}$,
将x=c代入y=±$\frac{b}{a}$x得y=±$\frac{bc}{a}$,则C(c,$\frac{bc}{a}$),D(c,-$\frac{bc}{a}$),
则|CD|=$\frac{2bc}{a}$,
∵|AB|≥$\frac{3}{5}$|CD|
∴$\frac{2{b}^{2}}{a}$≥$\frac{3}{5}$×$\frac{2bc}{a}$,即b≥$\frac{3}{5}$c,
则b2≥$\frac{9}{25}$c2=c2-a2,
即$\frac{16}{25}$c2≥a2,
则e2=$\frac{{c}^{2}}{{a}^{2}}$,则e≥$\frac{5}{4}$,
故选:B.
点评 本题主要考查双曲线离心率的计算,根据方程求出交点坐标,结合距离公式进行求解是解决本题的关键,属于中档题.


科目:高中数学 来源: 题型:填空题
 如图,球O的半径为5,一个内接圆台的两底面半径分别为3和4(球心O在圆台的两底面之间),则圆台的体积为$\frac{259π}{3}$.
如图,球O的半径为5,一个内接圆台的两底面半径分别为3和4(球心O在圆台的两底面之间),则圆台的体积为$\frac{259π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0,x∈R)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0,x∈R)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
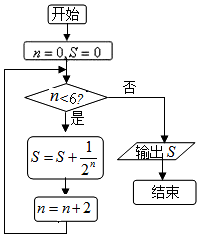
| A. | $\frac{21}{16}$ | B. | $\frac{85}{64}$ | C. | $\frac{63}{32}$ | D. | $\frac{127}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3≤x≤8,且x∈N | B. | 2≤x≤8,且x∈N | C. | 8≤x≤12,且x∈N | D. | 10≤x≤15,且x∈N |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p一定是真命题 | B. | 命题q一定是真命题 | ||
| C. | 命题q一定是假命题 | D. | 命题p也可以是假命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com