
分析 (1)求出C1,C2的普通方程,就两种情况分别求出P点坐标,根据距离列方程求出a,b,得出C1的普通方程;
(2)联立方程组求出P,R的坐标,利用距离公式计算|OP|和R到射线OP的距离即可求出三角形的面积.
解答 解:(1)曲线C1的普通方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,
曲线C2的直角坐标方程为(x-1)2+y2=1.
当α=0时,P(a,0),Q(2,0),∴a=1或3.
当$α=\frac{π}{2}$时,P(0,b),∴b=$\sqrt{3}$.
∵a>b>0,∴a=3,b=$\sqrt{3}$.
∴曲线C1的普通方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{3}=1$.
(2)把:$\left\{\begin{array}{l}{x=-t}\\{y=\sqrt{3}t}\end{array}\right.$代入方程(x-1)2+y2=1得2t2+t=0.
解得t=-$\frac{1}{2}$或t=0(舍).
∴R($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$).
当$α=\frac{π}{3}$时,射线l的方程为y=$\sqrt{3}x$(x≥0).即$\sqrt{3}x-y=0$.
联立方程组$\left\{\begin{array}{l}{y=\sqrt{3}x}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,解得x=$\frac{3\sqrt{10}}{10}$,y=$\frac{3\sqrt{30}}{10}$.即P($\frac{3\sqrt{10}}{10}$,$\frac{3\sqrt{30}}{10}$).
∴|OP|=$\frac{3\sqrt{10}}{5}$,R到射线OP的距离d=$\frac{|\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}|}{2}$=$\frac{\sqrt{3}}{2}$.
∴△OPR的面积S=$\frac{1}{2}•OP•d$=$\frac{1}{2}×\frac{3\sqrt{10}}{5}×\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{30}}{20}$.
点评 本题考查了参数方程,极坐标方程,普通方程的互化,直线与曲线的交点坐标,距离公式的应用,属于中档题.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | [-1,0) | C. | [-2,-1] | D. | [-2,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
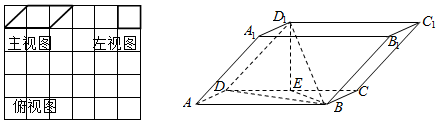
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{11}{10}$ | C. | $\frac{13}{14}$ | D. | $\frac{10}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
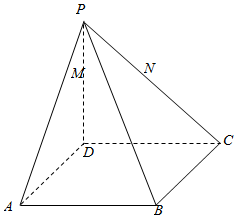 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,M,N分别为PD,PC上的点,且$\frac{PM}{MD}$=$\frac{PN}{NC}$,求证:MN∥AB.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,M,N分别为PD,PC上的点,且$\frac{PM}{MD}$=$\frac{PN}{NC}$,求证:MN∥AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com