
���� ��������$\left\{\begin{array}{l}{y=x+2}\\{\frac{{x}^{2}}{{a}^{2}}+{y}^{2}=1}\end{array}\right.$���ã�a2+1��x2+4a2x+3a2=0���ɴ�����Τ�ﶨ������Բ���壬�����֪�����������ԲC�ķ��̣�
������A��x1��y1����B��-x1��y1����Q��x0��y0������M��0��m����N��0��n��������֪���m=$\frac{{x}_{0}{y}_{1}-{x}_{1}{y}_{0}}{{x}_{0}-{x}_{1}}$��n=$\frac{{x}_{0}{y}_{1}+{x}_{1}{y}_{0}}{{x}_{0}+{x}_{1}}$���ɴ������mnΪ��ֵ1��
��� �⣺��������$\left\{\begin{array}{l}{y=x+2}\\{\frac{{x}^{2}}{{a}^{2}}+{y}^{2}=1}\end{array}\right.$���ã�a2+1��x2+4a2x+3a2=0��
��ֱ��y=x+2����Բ�й����㣬
���=16a4-4��a2+1����3a2��0�����a2��3����a$��\sqrt{3}$��
������Բ����֪|PF1|+|PF2|=2a��
�ʵ�a=$\sqrt{3}$ʱ��|PF1|+|PF2|ȡ����Сֵ��
��ʱ��ԲC�ķ���Ϊ$\frac{{x}^{2}}{3}+{y}^{2}=1$��
������A��x1��y1����B��-x1��y1����Q��x0��y0������M��0��m����N��0��n����
��kQA=kQM����$\frac{{y}_{0}-{y}_{1}}{{x}_{0}-{x}_{1}}$=$\frac{{y}_{0}-m}{{x}_{0}}$��
��${y}_{0}-m=\frac{{x}_{0}��{y}_{0}-{y}_{1}��}{{x}_{0}-{x}_{1}}$��
��m=${y}_{0}-\frac{{x}_{0}��{y}_{0}-{y}_{1}��}{{x}_{0}-{x}_{1}}$=$\frac{{x}_{0}{y}_{1}-{x}_{1}{y}_{0}}{{x}_{0}-{x}_{1}}$��
ͬ������n=$\frac{{x}_{0}{y}_{1}+{x}_{1}{y}_{0}}{{x}_{0}+{x}_{1}}$��
��mn=$\frac{{x}_{0}y-{x}_{1}{y}_{0}}{{x}_{0}-{x}_{1}}$•$\frac{{x}_{0}{y}_{1}+{x}_{1}{y}_{0}}{{x}_{0}+{x}_{1}}$=$\frac{{{x}_{0}}^{2}{{y}_{1}}^{2}-{{x}_{1}}^{2}{{y}_{0}}^{2}}{{{x}_{0}}^{2}-{{x}_{1}}^{2}}$��
��$\frac{{{x}_{0}}^{2}}{3}$+${{y}_{0}}^{2}$=1��$\frac{{{x}_{1}}^{2}}{3}+{{y}_{1}}^{2}=1$��
��${{y}_{0}}^{2}=1-\frac{{{x}_{0}}^{2}}{3}$��${{y}_{1}}^{2}=1-\frac{{{x}_{1}}^{2}}{3}$��
��mn=$\frac{{{x}_{0}}^{2}��1-\frac{{{x}_{1}}^{2}}{3}��-{{x}_{1}}^{2}��1-\frac{{{x}_{0}}^{2}}{3}��}{{{x}_{0}}^{2}-{{x}_{1}}^{2}}$=$\frac{{{x}_{0}}^{2}-{{x}_{1}}^{2}}{{{x}_{0}}^{2}-{{x}_{1}}^{2}}$=1��
��mnΪ��ֵ1��
���� ���⿼����Բ���̵���������ʵ��ֵ�ij˻��Ƿ�Ϊ��ֵ���ж���֤�������е��⣬����ʱҪ�������⣬ע������б�ʽ��Τ�ﶨ������Բ���̵����ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij����Ҫ�������������ֲ�Ʒ����Щ��ƷҪ��A��B��C��D���ֲ�ͬ���豸�ϼӹ��������չ涨����һ���ڣ�ÿ����Ʒ�ڸ��豸����Ҫ�ӹ���ʱ�䣬�����豸�����ʹ��ʱ�����±���
ij����Ҫ�������������ֲ�Ʒ����Щ��ƷҪ��A��B��C��D���ֲ�ͬ���豸�ϼӹ��������չ涨����һ���ڣ�ÿ����Ʒ�ڸ��豸����Ҫ�ӹ���ʱ�䣬�����豸�����ʹ��ʱ�����±���| �豸 | ��Ʒ��ÿ����Ҫ�ӹ�ʱ�� | ��Ʒ��ÿ����Ҫ�ӹ�ʱ�� | �豸�ʹ��ʱ�� |
| A | 2Сʱ | 2Сʱ | 12Сʱ |
| B | 1Сʱ | 2Сʱ | 8Сʱ |
| C | 4Сʱ | 0Сʱ | 16Сʱ |
| D | 0Сʱ | 4Сʱ | 12Сʱ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
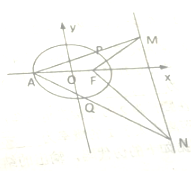 ��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����㣨1��$\frac{3}{2}$������������e=$\frac{1}{2}$������Բ�ҽ���F�����ഹֱ����ֱ���������߽��ڵ�M��N��AΪ��Բ���㣬����AM��AN����Բ��P��Q���㣮
��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����㣨1��$\frac{3}{2}$������������e=$\frac{1}{2}$������Բ�ҽ���F�����ഹֱ����ֱ���������߽��ڵ�M��N��AΪ��Բ���㣬����AM��AN����Բ��P��Q���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com