
分析 求出抛物线的普通方程,直线x+2y-12=0与该抛物线联立,可得x2+2x-24=0,x=4或-6,即可求出△ABF的面积.
解答 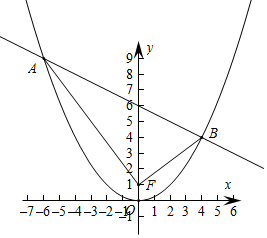 解:抛物线的参数方程为$\left\{\begin{array}{l}{x=2t}\\{y={t}^{2}}\end{array}\right.$(t为参数),普通方程为x2=4y,焦点为F(0,1),
解:抛物线的参数方程为$\left\{\begin{array}{l}{x=2t}\\{y={t}^{2}}\end{array}\right.$(t为参数),普通方程为x2=4y,焦点为F(0,1),
直线x+2y-12=0与该抛物线联立,可得x2+2x-24=0,∴x=4或-6,
直线x+2y-12=0,令x=0,可得y=6
∴△ABF的面积为$\frac{1}{2}×(6-1)×(4+6)$=25,
故答案为25.
点评 本题考查抛物线的参数方程,考查直线与抛物线的位置关系,考查三角形面积的计算,属于中档题.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{35}{16}$ | B. | $\frac{35}{8}$ | C. | $\frac{35}{4}$ | D. | 105 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (∞,-1)∪(2,+∞) | B. | [-1,2] | C. | (∞,-1]∪[2,+∞) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
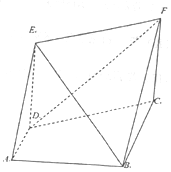 如图所示,直角梯形ABCD中,AD∥BC,AD⊥AB,AB=BC=2AD=2,四边形EDCF为矩形,CF=$\sqrt{3}$,平面EDCF⊥平面ABCD.
如图所示,直角梯形ABCD中,AD∥BC,AD⊥AB,AB=BC=2AD=2,四边形EDCF为矩形,CF=$\sqrt{3}$,平面EDCF⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于直线$x=\frac{π}{3}$对称 | B. | 关于直线$x=\frac{π}{6}$对称 | ||
| C. | 关于点$(\frac{π}{3},0)$对称 | D. | 关于点$(\frac{π}{6},0)$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2023×2017 | B. | 2023×2016 | C. | 1008×2023 | D. | 2017×1008 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com