
【题目】已知函数f(x)=ax2﹣x+2a﹣1(a>0).
(1)若f(x)在区间[1,2]为单调增函数,求a的取值范围;
(2)设函数f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式;
(3)设函数 ![]() ,若对任意x1 , x2∈[1,2],不等式f(x1)≥h(x2)恒成立,求实数a的取值范围.
,若对任意x1 , x2∈[1,2],不等式f(x1)≥h(x2)恒成立,求实数a的取值范围.
【答案】
(1)解:∵函数f(x)=ax2﹣x+2a﹣1(a>0)的图象是开口朝上,且以直线x= ![]() 为对称轴的抛物线,
为对称轴的抛物线,
若f(x)在区间[1,2]为单调增函数
则 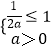 ,
,
解得: ![]()
(2)解:①当0< ![]() <1,即a>
<1,即a> ![]() 时,f(x)在区间[1,2]上为增函数,
时,f(x)在区间[1,2]上为增函数,
此时g(a)=f(1)=3a﹣2
②当1≤ ![]() ≤2,即
≤2,即 ![]() 时,f(x)在区间[1,
时,f(x)在区间[1, ![]() ]是减函数,在区间[
]是减函数,在区间[ ![]() ,2]上为增函数,
,2]上为增函数,
此时g(a)=f( ![]() )=
)= ![]()
③当 ![]() >2,即0<a<
>2,即0<a< ![]() 时,f(x)在区间[1,2]上是减函数,
时,f(x)在区间[1,2]上是减函数,
此时g(a)=f(2)=6a﹣3
综上所述: 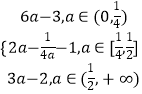
(3)解:对任意x1,x2∈[1,2],不等式f(x1)≥h(x2)恒成立,
即f(x)min≥h(x)max,
由(2)知,f(x)min=g(a)
又因为函数 ![]() ,
,
所以函数h(x)在[1,2]上为单调减函数,所以 ![]() ,
,
①当 ![]() 时,由g(a)≥h(x)max得:
时,由g(a)≥h(x)max得: ![]() ,解得
,解得 ![]() ,(舍去)
,(舍去)
②当 ![]() 时,由g(a)≥h(x)max得:
时,由g(a)≥h(x)max得: ![]() ,即8a2﹣2a﹣1≥0,
,即8a2﹣2a﹣1≥0,
∴(4a+1)(2a﹣1)≥0,解得 ![]()
所以 ![]()
③当 ![]() 时,由g(a)≥h(x)max得:
时,由g(a)≥h(x)max得: ![]() ,解得
,解得 ![]() ,
,
所以a ![]()
综上所述:实数a的取值范围为 ![]()
【解析】(1)若f(x)在区间[1,2]为单调增函数,则 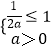 ,解得a的取值范围;(2)分类讨论给定区间与对称轴的关系,分析出各种情况下g(x)的表达式,综合讨论结果,可得答案;(3)不等式f(x1)≥h(x2)恒成立,即f(x)min≥h(x)max , 分类讨论各种情况下实数a的取值,综合讨论结果,可得答案.
,解得a的取值范围;(2)分类讨论给定区间与对称轴的关系,分析出各种情况下g(x)的表达式,综合讨论结果,可得答案;(3)不等式f(x1)≥h(x2)恒成立,即f(x)min≥h(x)max , 分类讨论各种情况下实数a的取值,综合讨论结果,可得答案.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:高中数学 来源: 题型:
【题目】轮船![]() 从某港口将一些物品送到正航行的轮船
从某港口将一些物品送到正航行的轮船![]() 上,在轮船
上,在轮船![]() 出发时,轮船
出发时,轮船![]() 位于港口
位于港口![]() 北偏西
北偏西![]() 且与
且与![]() 相距20海里的
相距20海里的![]() 处,并正以30海里的航速沿正东方向匀速行驶,假设轮船
处,并正以30海里的航速沿正东方向匀速行驶,假设轮船![]() 沿直线方向以
沿直线方向以![]() 海里/小时的航速匀速行驶,经过
海里/小时的航速匀速行驶,经过![]() 小时与轮船
小时与轮船![]() 相遇.
相遇.
(1)若使相遇时轮船![]() 航距最短,则轮船
航距最短,则轮船![]() 的航行速度大小应为多少?
的航行速度大小应为多少?
(2)假设轮船![]() 的最高航速只能达到30海里/小时,则轮船
的最高航速只能达到30海里/小时,则轮船![]() 以多大速度及什么航行方向才能在最短时间与轮船
以多大速度及什么航行方向才能在最短时间与轮船![]() 相遇,并说明理由.
相遇,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且Sn=2n2+n,n∈N,数列{bn}满足an=4log2bn+3,n∈N.
(1)求an,bn;
(2)求数列{anbn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,过点
,过点![]() 的动直线与椭圆相交于
的动直线与椭圆相交于![]() ,
, ![]() 两点,当直线
两点,当直线![]() 平行于
平行于![]() 轴时,直线
轴时,直线![]() 被椭圆截得的线段长为
被椭圆截得的线段长为![]() .
.
(1)求椭圆的方程;
(2)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)记椭圆的右顶点为![]() ,点
,点![]() (
(![]() )在椭圆上,直线
)在椭圆上,直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 交
交![]() 轴于点
轴于点![]() .问:
.问: ![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() (
(![]() 为坐标原点)?若存在,求点
为坐标原点)?若存在,求点![]() 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,函数f(x)=lg(4﹣x)﹣ ![]() 的定义域为集合A,集合B={x|﹣2<x<a}.
的定义域为集合A,集合B={x|﹣2<x<a}.
(1)求集合UA;
(2)若A∪B=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() ,双曲线
,双曲线![]() :
: ![]() ,若以
,若以![]() 的长轴为直径的圆与
的长轴为直径的圆与![]() 的一条渐近线交于A、B两点,且椭圆
的一条渐近线交于A、B两点,且椭圆![]() 与该渐近线的两交点将线段AB三等分,则
与该渐近线的两交点将线段AB三等分,则![]() 的离心率是( )
的离心率是( )
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a﹣ ![]() 为奇函数.
为奇函数.
(1)求a的值;
(2)试判断函数f(x)在(﹣∞,+∞)上的单调性,并证明你的结论;
(3)若对任意的t∈R,不等式f[t2﹣(m﹣2)t]+f(t2﹣m+1)>0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孝感车天地关于某品牌汽车的使用年限![]() (年)和所支出的维修费用
(年)和所支出的维修费用![]() (千元)由如表的统计资料:
(千元)由如表的统计资料:
| 2 | 3 | 4 | 5 | 6 |
| 2.1 | 3.4 | 5.9 | 6.6 | 7.0 |
(1)画出散点图并判断使用年限与所支出的维修费用是否线性相关;如果线性相关,求回归直线方程;
(2)若使用超过8年,维修费用超过1.5万元时,车主将处理掉该车,估计第10年年底时,车主是否会处理掉该车?
( )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com