
| 节能意识弱 | 节能意识强 | 总计 | |
| 20至50岁 | 45 | 9 | 54 |
| 大于50岁 | 10 | 36 | 46 |
| 总计 | 55 | 45 | 100 |
| 1 |
| 9 |
| 9 |
| 54 |
| 36 |
| 46 |
| 36 |
| 45 |
| 36 |
| 45 |
| 9 |
| 45 |
| 4 |
| 10 |
| 2 |
| 5 |
| 2 |
| 5 |


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
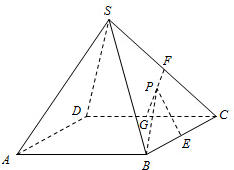 如图,正四棱锥S-ABCD中,SA=AB,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点.
如图,正四棱锥S-ABCD中,SA=AB,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点.查看答案和解析>>
科目:高中数学 来源: 题型:
| A、(-∞,-6] |
| B、[6,+∞) |
| C、(-∞,-6]∪[6,+∞) |
| D、[-6,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:
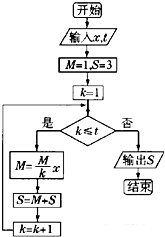 执行如图所示的程序框图,如果输入x,t的值均为2,最后输出S的值为n,在区间[0,10]上随机选取一个数D,则D≤n的概率为( )
执行如图所示的程序框图,如果输入x,t的值均为2,最后输出S的值为n,在区间[0,10]上随机选取一个数D,则D≤n的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com