Question

6．在△ABC中，边a、b、c分别是内角A、B、C所对的边，且满足2sinB=sinA+sinC，设B的最大值为B₀．
（1）求B₀的值；
（2）当B=B₀，a=3，b=6时，又$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{DB}$，求CD的长．

Answer 1

分析 （1）由题设及正弦定理知，2b=a+c，即$b=\frac{a+c}{2}$，由余弦定理，基本不等式可得cosB≥$\frac{1}{2}$，由B为锐角，利用余弦函数的单调性即可解得B的最大值${B_0}=\frac{π}{3}$．
（2）由已知及余弦定理可求c的值，又$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{DB}$，可得BD=$\frac{2}{3}$AB=1+$\sqrt{13}$，在△BCD中，由余弦定理即可解得CD的值．

解答 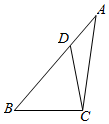（本题满分为12分）
解：（1）由题设及正弦定理知，2b=a+c，即$b=\frac{a+c}{2}$
由余弦定理知，$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{{{a^2}+{c^2}-{{（\frac{a+c}{2}）}^2}}}{2ac}=\frac{{3（{a^2}+{c^2}）-2ac}}{8ac}≥\frac{3（2ac）-2ac}{8ac}=\frac{1}{2}$，
∵y=cosx在（0，π）上单调递减，
∴B的最大值${B_0}=\frac{π}{3}$…（6分）
（2）∵$B={B_0}=\frac{π}{3}，a=3，b=6$，
∴由b²=a²+c²-2accosB，可得：36=9+c²-2×3×c×$\frac{1}{2}$，解得：c=$\frac{3+3\sqrt{13}}{2}$，
∵又$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{DB}$，
∴BD=$\frac{2}{3}$AB=$\frac{2}{3}$×$\frac{3+3\sqrt{13}}{2}$=1+$\sqrt{13}$，
∴在△BCD中，由余弦定理可得：CD=$\sqrt{B{D}^{2}+B{C}^{2}-2BD•BC•cosB}$=$\sqrt{（1+\sqrt{13}）^{2}+9-2×3×（1+\sqrt{13}）×\frac{1}{2}}$=$\sqrt{20-\sqrt{13}}$…（12分）

点评 本题主要考查了正弦定理，余弦定理，平面向量及其运算，余弦函数的单调性在解三角形中的综合应用，考查了计算能力和转化思想，属于中档题．