
【题目】在直角三角形![]() 中,
中,![]() ,点
,点![]() 分别在边
分别在边![]() 和
和![]() 上(
上(![]() 与
与![]() 不重合),将
不重合),将![]() 沿
沿![]() 翻折,
翻折,![]() 变为
变为![]() ,使顶点
,使顶点![]() 落在边
落在边![]() 上(
上(![]() 与
与![]() 不重合),设
不重合),设![]() .
.

(1)若![]() ,求线段
,求线段![]() 的长度;
的长度;
(2)用![]() 表示线段
表示线段![]() 的长度;
的长度;
(3)求线段![]() 长度的最小值
长度的最小值
科目:高中数学 来源: 题型:
【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
文艺节目 | 新闻节目 | 总计 | |
20至40岁 | 42 | 16 | 58 |
大于40岁 | 18 | 24 | 42 |
总计 | 60 | 40 | 100 |
(1)用分层抽样方法在收看新闻节目的观众中随机抽取5名观众,则大于40岁的观众应该抽取几名?
(2)由表中数据分析,收看新闻节目的观众是否与年龄有关?
(3)在第(1)中抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率.
(提示:![]() ,其中
,其中![]() .当
.当![]() 时,有
时,有![]() 的把握判定两个变量有关联;当
的把握判定两个变量有关联;当![]() 时,有
时,有![]() 的把握判定两个变量有关联;当
的把握判定两个变量有关联;当![]() 时,有
时,有![]() 的把握判定两个变量有关联.)
的把握判定两个变量有关联.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设X~N(μ1,![]() ),Y~N(μ2,
),Y~N(μ2,![]() ),这两个正态分布密度曲线如图所示,下列结论中正确的是 ( )
),这两个正态分布密度曲线如图所示,下列结论中正确的是 ( )

A. P(Y≥μ2)≥P(Y≥μ1)
B. P(X≤σ2)≤P(X≤σ1)
C. 对任意正数t,P(X≥t)≥P(Y≥t)
D. 对任意正数t,P(X≤t)≥P(Y≤t)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题的真假:
(1)点P到圆心O的距离大于圆的半径是点P在![]() 外的充要条件;
外的充要条件;
(2)两个三角形的面积相等是这两个三角形全等的充分不必要条件;
(3)![]() 是
是![]() 的必要不充分条件;
的必要不充分条件;
(4)x或y为有理数是xy为有理数的既不充分又不必要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,四边形![]() 为正方形,延长
为正方形,延长![]() 至
至![]() ,使得
,使得![]() ,将四边形
,将四边形![]() 沿
沿![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() ,如图2.
,如图2.

(1)求证:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(3)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A,B是R中两个子集,对于![]() ,定义:
,定义: 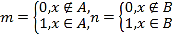 .①若
.①若![]() ;则对任意
;则对任意![]() ;②若对任意
;②若对任意![]() ,则
,则![]() ;③若对任意
;③若对任意![]() ,则A,B的关系为
,则A,B的关系为![]() .上述命题正确的序号是______. (请填写所有正确命题的序号)
.上述命题正确的序号是______. (请填写所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com