
分析 (Ⅰ)设从甲盒中取出的卡片标号为x,从乙盒中取出的卡片标号为y,用(x,y)表示抽取结果,利用列举法能求出取出的两张卡片标号之积能被3整除的概率.
(Ⅱ) 设“小王胜出”为事件B,不妨设小王取出的结果为(3,4),利用列举法能求出小王胜出的概率.
解答 (本小题满分12分)
解:(Ⅰ)设从甲盒中取出的卡片标号为x,从乙盒中取出的卡片标号为y,
用(x,y)表示抽取结果,则所有可能的结果有16种,即
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4).…(2分)
(Ⅰ) 设“取出的两张卡片标号的数字之积能被3整除”为事件A,
则A={(1,3),(3,1),(2,3),(3,2),(3,3),(3,4),(4,3)}
事件A由7个基本事件组成,故所求概率P(A)=$\frac{7}{16}$;…(8分)
(Ⅱ) 设“小王胜出”为事件B,不妨设小王取出的结果为(3,4),
则小李抽出的两张卡片的所有结果有9种,即
(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(4,1),(4,2),(4,3),
事件B由8个基本事件组成,故所求概率$P(B)=\frac{8}{9}$…(12分)
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 平行四边形 | B. | 矩形 | C. | 正方形 | D. | 菱形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\overrightarrow a$•$\overrightarrow b$)•$\overrightarrow c$=$\overrightarrow a$•($\overrightarrow b$•$\overrightarrow c$) | B. | 若$\overrightarrow a$•$\overrightarrow b$=$\overrightarrow a$•$\overrightarrow c$,则$\overrightarrow b$=$\overrightarrow c$ | ||
| C. | |$\overrightarrow a$•$\overrightarrow b$|=|$\overrightarrow a$|•|$\overrightarrow b$| | D. | 若$|\overrightarrow a$+$\overrightarrow b$|=|$\overrightarrow a$-$\overrightarrow b$|,则$\overrightarrow a$•$\overrightarrow b$=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于直线x=$\frac{π}{12}$对称 | B. | 关于直线x=$\frac{5π}{12}$对称 | ||
| C. | 关于点($\frac{π}{12}$,0)对称 | D. | 关于点($\frac{5π}{12}$,0)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧(¬q) | C. | (¬p)∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
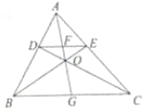 如图,在△ABC中,作平行于BC的直线交AB于D,交AC于E,如果BE和CD相交于点O,AO和DE相交于点F,AO的延长线和BC相交于G.证明:
如图,在△ABC中,作平行于BC的直线交AB于D,交AC于E,如果BE和CD相交于点O,AO和DE相交于点F,AO的延长线和BC相交于G.证明:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com