
分析 (1)由等差数列的性质可知:a+3a=2×4,即可求得a1=a=2,d=a2-a1=2,代入前n项和公式即可求得k的值;
(2)由bn=$\frac{1}{{S}_{n}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,采用“裂项法”即可求得数列{bn}的前n项和.
解答 解:(1)等差数列为{an}的前三项分别为:a1=a,a2=4,a3=3a,
∴a+3a=2×4,解得:a1=a=2,公差d=a2-a1=2,将Sk=90,
代入公式Sk=ka1+$\frac{k(k+1)}{2}•d$,解得:k=9,
∴a=2,k=9;
(2)由 (1)可知:Sn=2n+$\frac{n(n-1)}{2}$×2=n(n+1),
bn=$\frac{1}{{S}_{n}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
数列{bn}的前n项和$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+…+$\frac{1}{{S}_{n}}$=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{n(n+1)}$,
=(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+…+($\frac{1}{n}$-$\frac{1}{n+1}$),
=1-$\frac{1}{n+1}$,
=$\frac{n}{n+1}$,
数列{bn}的前n项和$\frac{n}{n+1}$.
点评 本题考查等差数列的性质,考查等差数列前n项和公式,考查“裂项法”求数列的前n项和公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3≤k≤2 | B. | k≥2或k≤-3 | C. | -2≤k≤3 | D. | k≥3或k≤-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
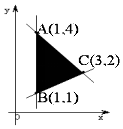 已知平面区域如图所示,z=mx+y在平面区域内取得最 大值的最优解有无数多个,则m的值为( )
已知平面区域如图所示,z=mx+y在平面区域内取得最 大值的最优解有无数多个,则m的值为( )| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,1) | B. | ($\frac{3}{2}$,$\frac{9}{4}$) | C. | ($\frac{2}{3}$,$\frac{4}{9}$) | D. | (2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com