
分析 (1)由a2=$\frac{2}{3}$,2an-an+1=0,求出数列{an}的首项,并得到数列{an}是以$\frac{1}{3}$为首项,以2为公比的等比数列,由等比数列的通项公式得答案;
(2)由已知结合数列{(2n-1)an+1}是等差数列求其公差,进一步得到数列{(2n-1)an+1}的通项公式,代入{$\frac{n}{{a}_{n}}$},再由等差数列的前n项和得答案.
解答 解:(1)由a2=$\frac{2}{3}$,2an-an+1=0,得${a}_{1}=\frac{1}{3}$,且$\frac{{a}_{n+1}}{{a}_{n}}=2$.
∴数列{an}是以$\frac{1}{3}$为首项,以2为公比的等比数列,
则${a}_{n}=\frac{1}{3}•{2}^{n-1}$;
(2)∵a2=$\frac{2}{3}$,a4=$\frac{4}{7}$,且数列{(2n-1)an+1}是等差数列,
则数列{(2n-1)an+1}的公差为d=$\frac{[(2×4-1)×\frac{4}{7}+1]-[(2×2-1)×\frac{2}{3}+1]}{4-2}$=1.
∴(2n-1)an+1=(2×2-1)×$\frac{2}{3}$+1+(n-2)×1=n+1,
∴${a}_{n}=\frac{n}{2n-1}$,
则$\frac{n}{{a}_{n}}$=$\frac{n}{\frac{n}{2n-1}}=2n-1$.
∴Tn=1+3+5+…+(2n-1)=$\frac{[1+(2n-1)]×n}{2}={n}^{2}$.
点评 本题考查数列递推式,考查了等比数列通项公式的求法,考查等差数列的通项公式,属中档题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -2$\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,$\frac{1}{3}$) | C. | [0,+∞) | D. | (-$\frac{1}{2}$,-$\frac{1}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
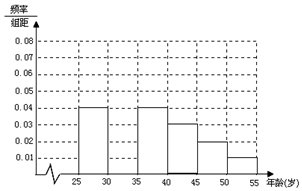 智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图:
智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com