
分析 (1)连接OQ、OP,则△OQP为直角三角形,利用|PQ|=|PA|,求P点的轨迹方程;
(2)表示出|PQ|,利用配方法求|PQ|的最小值;
(3)以P为圆心的圆与圆O有公共点,半径最小时为与圆O相切的情形,而这些半径的最小值为圆O到直线l的距离减去圆O的半径,即可求出半径最小的圆的方程.
解答 解 (1)连接OQ、OP,则△OQP为直角三角形,
又|PQ|=|PA|,
所以|OP|2=|OQ|2+|PQ|2=5+|PA|2,
所以a2+b2=5+(a-4)2+(b-3)2,故4a+3b-15=0.
(2)由|PQ|2=|OP|2-5=a2+b2-5=$\frac{25}{9}$(a-$\frac{12}{5}$)2+4,
得|PQ|min=4.
(3)以P为圆心的圆与圆O有公共点,半径最小时为与圆O相切的情形,而这些半径的最小值为圆O到直线l的距离减去圆O的半径,圆心P为过原点且与l垂直的直线l′与l的交点P0,所以r=3-$\sqrt{5}$,
又l′:3x-4y=0,联立l:4x+3y-15=0得P0($\frac{12}{5}$,$\frac{9}{5}$).
所以所求圆的方程为(x-$\frac{12}{5}$)2+(y-$\frac{9}{5}$)2=(3-$\sqrt{5}$)2.
点评 本题考查轨迹方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2或$-\frac{5}{2}$ | C. | 2或-2 | D. | 2或-2或$-\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 26 | C. | 28 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
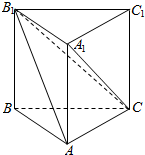 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=BB1=1,B1C=2.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=BB1=1,B1C=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
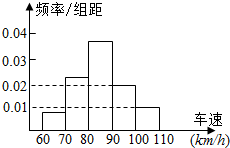 在某路段车辆检测点,随机抽取了400辆过往汽车进行车速检测,检测结果的频率分布直方图如图所示,则这400辆汽车中车速大于90km/h的汽车约有( )
在某路段车辆检测点,随机抽取了400辆过往汽车进行车速检测,检测结果的频率分布直方图如图所示,则这400辆汽车中车速大于90km/h的汽车约有( )| A. | 12辆 | B. | 80辆 | C. | 100辆 | D. | 120辆 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com