【题目】如图，四棱锥
的底面
是正方形，侧棱
底面，
，
是
的中点.
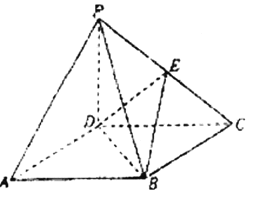
（1）证明：
平面
；
（2）求二面角
的余弦值；
（3）若点
在线段
（不包含端点）上，且直线
平面
，求线段
的长.
【答案】（1）证明见解析（2）
（3）
【解析】
（1）建立以
为坐标原点，分别以
所在直线为
轴、
轴、
轴的空间直角坐标系，再标出点的坐标，利用空间向量的应用即可得证；
（2）求出平面
的一个法向量，平面
的一个法向量，再利用数量积公式求解即可；
（3）假设棱
上存在点
，使
平面
，由
求解即可.
证明：（1）以为坐标原点，分别以所在直线为轴、轴、轴建立空间直角坐标系，
设
，则
，
，
，
则
，
，
，
设
是平面的一个法向量，
则由
，得
，取
，得
.
，
，
又
平面，
平面.
（2）解：由（1）知是平面的一个法向量，
又
是平面的一个法向量.
设二面角
的平面角为
，由图可知
，
,
故二面角的平面角的余弦值为.
（3）假设棱上存在点，使平面，
设
，
则
，
，
，
，
由得
，
解得
，
，
则
.
轻松课堂标准练系列答案科目：高中数学 来源： 题型：
【题目】条形码是由一组规则排列的条、空及其对应的代码组成，用来表示一定的信息，我们通常见的条形码是“
”通用代码，它是由从左到右排列的
个数字（用
，
，…，
表示）组成，这些数字分别表示前缀部分、制造厂代码、商品代码和校验码，其中是校验码，用来校验前
个数字代码的正确性．图（1）是计算第位校验码的程序框图，框图中符号
表示不超过
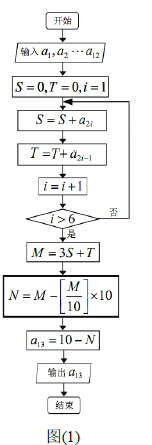
的最大整数（例如
）．现有一条形码如图（2）所示（
），其中第
个数被污损，那么这个被污损数字
是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下表是我省某地区2012年至2018年农村居民家庭年纯收入
（单位：万元）的数据如下表：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
年纯收入 | 2 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
（1）求关于
的线性回归方程；
（2）利用（1）中的回归方程，分析2012年至2018年该地区农村居民家庭年纯收入的变化情况，并预测该地区2019年农村居民家庭年纯收入（结果精确到0.1）。
附：回归直线的斜率和截距的最小二乘法估计公式分别为：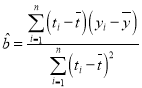
，
。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“既要金山银山，又要绿水青山”。某风景区在一个直径
为
米的半圆形花圆中设计一条观光线路。打算在半圆弧上任选一点
（与
不重合），沿
修一条直线段小路，在路的两侧（注意是两侧）种植绿化带；再沿弧
修一条弧形小路，在小路的一侧（注意是一侧）种植绿化带，小路与绿化带的宽度忽略不计。
（1）设
（弧度），将绿化带的总长度表示为
的函数
；
（2）求绿化带的总长度的最大值。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，以坐标原点为极点，
轴正半轴为极轴建立极坐标系，曲线
的极坐标方程是
，曲线
的参数方程为：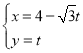
（
为参数）.
（1）求曲线，的直角坐标方程；
（2）设曲线，交于点
，
，已知点
，求
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
,
（Ⅰ）若
在
上的最大值为
，求实数b的值；
（Ⅱ）若对任意x∈[1，e]，都有
恒成立，求实数a的取值范围；
（Ⅲ）在（Ⅰ）的条件下，设
，对任意给定的正实数a，曲线y=F（x）上是否存在两点P、Q，使得△POQ是以O（O为坐标原点）为直角顶点的直角三角形，且此三角形斜边中点在y轴上？请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
